電気抵抗値の四端子測定法の原理を簡単に説明

電流の通りやすさ通り難さを表す抵抗値は、一般的には、テスターと言われる回路計で測定します。
テスターで抵抗値を測ったことがある方は、測定棒の当て方で抵抗値の表示が変わったり、 或いは、テスターの本体と測定棒を繋いでいるコードが持つ電気抵抗値は補正されているのだろうか？などと思ったりしたことは無いでしょうか。
抵抗値を正確に求めようとすると気になります。特に、測定する対象の抵抗値が小さいときは尚更です。 私は、自動車用鉛バッテリーの内部抵抗を測るために四端子測定法を用いた測定器を使ってみました。⇒ 安価な自動車用鉛バッテリーテスター(AE300)で測定してみた

測定器と測定する対象を繋げるコードの電気抵抗、そのコードと測定する対象を繋げるときの接触抵抗が測定値に与える影響を少なくする測定法に「四端子測定法」があります。
四端子測定法は下図の様になっています。

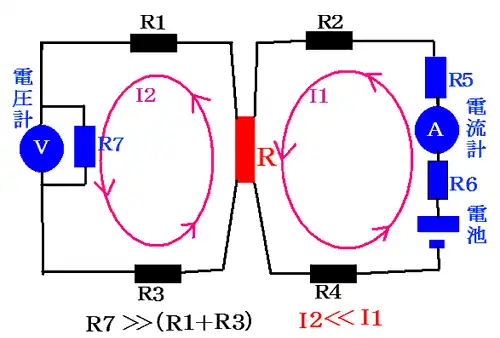
図中央の赤い四角Ｒが抵抗値を求めたい物です。
赤い四角Ｒには、図左側の電圧計に繋がる電気コード２本と、図右側の電流計と電池に繋がる電気コード２本が繋がっています。
それらの電気コードが持つ抵抗と測定したい物に繋いだときの接触抵抗を合わせた抵抗が、それぞれ、Ｒ１，Ｒ２，Ｒ３，Ｒ４です。
Ｒ５は電流計の内部抵抗、Ｒ６は電池の内部抵抗、Ｒ７は電圧計の内部抵抗です。

この回路(四端子測定法)で、赤い四角で示した抵抗Ｒを求めるには、キルヒホフの法則を使います。
具体的には、左側の回路では、左側の回路の抵抗を流れる電流によって起きる電圧は０になります。
右側の回路では、左側の回路の抵抗を流れる電流によって起きる電圧と電池の電圧が等しくなります。
ただし、両回路に共通の抵抗Ｒ(抵抗値を求める対象物)に流れる電流は、電流の向きを図の様に仮定すると、(Ｉ１－Ｉ２)です。

キルヒホフの法則で抵抗Ｒを求めるのは数式に強い方にお願いして、ここでは四端子測定法のしくみの理解に重点を置きます。
左側の回路にある電圧計は内部抵抗Ｒ７が非常に大きい物を使います。
すると、電気コードの抵抗と接触抵抗Ｒ１，Ｒ３は小さい値なので、電圧計の内部抵抗Ｒ７に吸収されてしまいます。
たとえば、電気コードと接触抵抗の合計が１Ωと電圧計の内部抵抗１００００００Ωを直列接続した回路では、 電気コードと接触抵抗の合計が１Ωでも２Ωでも計算では切り捨てられる違いでしかありません。
１０００００１Ωと１０００００２Ωの違いです

右側の電流計と電池の回路では、電気コードの抵抗と接触抵抗Ｒ２，Ｒ４がどのような値でも 直列に入れた電流計が電流Ｉ１を測定しているので影響はありません。

左側の回路を流れる電流Ｉ２は、回路に直列に入っている電圧計の内部抵抗が非常に大きいので非常に小さくなります。
すると、赤い四角で示した抵抗Ｒに流れる電流はＩ１だけ考えればよいことになります。
電流Ｉ１によって赤い四角で示した抵抗Ｒの両端に生じる電圧は、左側の電圧計で測定できるのでこの値をＥとすれば、 オームの法則から
Ｅ＝Ｉ１×Ｒ
Ｒ＝Ｅ÷Ｉ１
Ｉ１は右側の電流計の値なので、 求める抵抗Ｒの値は、電圧計の値÷電流計の値　となります。