抵抗を並列接続した合成抵抗値をキルヒホッフの法則で求める方法

キルヒホフの法則（またはキルヒホッフの法則）を使って電気抵抗値が$R_{a}$と$R_{b}$の二つの抵抗を並列に接続したときの合成抵抗値の求め方です。
合成抵抗値は $$\frac{R_{a} R_{b}}{R_{a}+R{b}}$$ です。
この公式の求め方を考えてみましょう。
下図のような電気回路を作り、電流（赤線）がこのように流れていると仮定します。

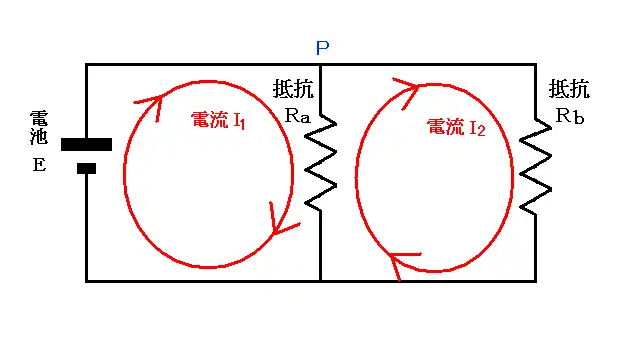
左側が$I_{1}$ 右側が$I_{2}$ です。
実際に図で示した向きに流れているかはこの段階では判りませんが、実際の電流の向きは計算すると判明します。

この回路に キルヒホフの法則(キルヒホッフの法則) を適用します。

キルヒホフの法則は電流と電圧の法則があります。
電流の法則は、たとえば上図Ｐ点に流れ込む電流とＰ点から出る電流の和は$0$というものです。
電流は一箇所に留まっていられないものですから、 入る量と出る量の和が$0$になるのは当然です。

電圧の法則は、閉じた電気回路内で電流を一方向にとったときに、 各部に起きる電圧の和は$0$になるというものです。
上図の電気回路で言うと、左側の電池と抵抗$R_{a}$で作られた閉じた回路においては、抵抗$R_{a}$の両端の電圧と電池の電圧を足すと$0$になります。
右側の、抵抗$R_{a}$と抵抗$R_{b}$で作られた閉じた回路においては、 抵抗$R_{a}$の両端の電圧と、抵抗$R_{b}$の両端の電圧を足すと$0$になります。
このとき、電流の向きを考えることが重要です。
電流の向きが逆になれば、プラスだった点がマイナスになり、 マイナスだった点がプラスになるので、各部の電圧を足したら$0$ということになるのです。

では、実際に計算してみます。
求めたいのは抵抗$R_{a}$と抵抗$R_{b}$を並列に接続したときの合成抵抗です。
このときの合成抵抗$R$は、オームの法則から$R = E/I_{1}$ ですから、$I_{1}$を求めます。 上図の左側の閉じた回路にキルヒホフの電圧法則を適用します。
ここでは $I_{1}$ の電流の向きを正として

次に右側の閉じた回路にもキルヒホフの電圧法則を適用します。
ここでも、$I_{1}$の電流の向きを正とします。

このように、キルヒホフの法則は、電気回路・電子回路の解析に便利に使えるものです。
回路が複雑になると方程式がたくさん出来ますが、連立方程式はコンピューターで解くのに適しています。

ところで、抵抗の並列接続はもっと簡単に求められます。
抵抗$R_{a}$の両端の電圧は、抵抗$R_{a}$を流れる電流$I_{1}$ 、抵抗$R_{b}$を流れる電流$I_{2}$とし、 二つの抵抗の両端の電圧は電池の電圧$E$と等しく、抵抗を流れる電流の向きも同じなので