トランシーバー用の無給電中継の考察
VHFやUHF帯の電波は直進性が強いために、送受信間に建物などの障害物があると極端に通信距離が短くなってしまいます。
そこで、広域で使う業務無線などでは山頂や高層建築物の上に中継局を置いています。
このような中継局は、送信周波数Aで発信された電波を受信すると、その信号を周波数Bに再送信します。
小規模の中継局というか機器は、従業員が連絡用に特定小電力トランシーバーを使っている店などで見ることが出来ます。
これらの中継局や機器は受信や再送信時に外部から電気を供給して信号を増幅しています。
これから考えてみるのは、外部からの電気の力を借りない中継器です。
下図のように、トランシーバーのアンテナ1からの電波をアンテナ2で受信し、 少し離れた所まで同軸ケーブルで送って、そこで再びアンテナ3から放射させ、トランシーバーのアンテナ4で受信するものです。
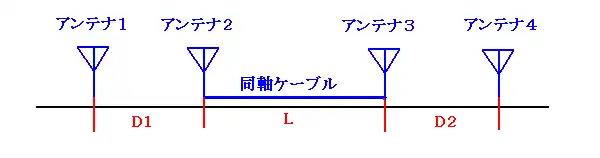
トランシーバーには送信出力10mWの特定小電力を使います。
1mW=0dBとすると、10dBです。
特定小電力トランシーバーのアンテナは貧弱ですから、アンテナから放射される電力は2dB減少すると勝手に仮定します。
すると、実際にアンテナから放射される電力は8dB(6.3mW)です。
この電力を距離D1離れているアンテナ2で受け取ります。
ここでは先行きが心配なので、D1=1mとします。
アンテナ1から放射される電波が全方位に向けて放射されるとすると、 半径1mの球体の表面全てで集めた電力が8dBということですから、アンテナ2で受けられる面積÷球体の表面積×アンテナ1が放射する電力がアンテナ2に入ることになります。
ところで、アンテナの能力を示す概念に実効面積があります。
電波望遠鏡や衛星中継用のパラボラアンテナを見ると一目瞭然ですが、アンテナというのは微弱な電波を広い面積で集めるもので、ダイポールアンテナのような線状アンテナでも同じです。
この電波を集められる面の大きさを実効面積といいます。
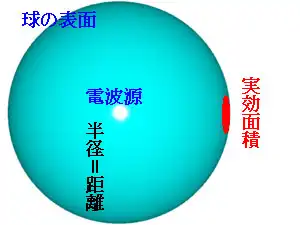
ダイポールアンテナの場合は、波長をλで表すと、近似的にはλ/2×λ/4 で表されます。
ですから、アンテナ2で受けられる面積は、λ/2×λ/4になります。
球体の表面積は、半径をD1とすると、4×π×D1×D1ですから、アンテナ2が受けとる電力は
(λ/2×λ/4)/(4×π×D1×D1)×アンテナ1が放射する電力
となります。周波数を422MHz、D1を1m、放射する電力を6.3mWとすると
0.0317mW(-15dB)になります。
この電力を同軸ケーブルでアンテナ3に送り込みますが、ケーブルには損失があります。
低損失同軸ケーブルは高価なのでどこにでもあるテレビ受信用の5C-2Vを5m使ってみます。
ケーブルでの損失は約-1dBです。
ですから、0.025mW(-16dB)がアンテナ3に送り込まれます。
アンテナ3にダイポールアンテナを使うと、アンテナ利得が約2.14dBあるので、アンテナ3から放射される電力は、0.041mW(-14dB)になります。
今度はD2を求めるために特定小電力トランシーバーの受信能力を推定します。
スキー場で1から2km通話可能と書いてあることが多いので、送受信間に障害物が無ければ1km通話可能として。
受信アンテナに届く電界の計算は、直接アンテナに届く直接波と、大地に反射して届く反射波の合成で求めますが、反射波を無視して球体の表面積とアンテナの実効面積を使って求めてみます。
送信受信アンテナ共に損失は-2dBです。
計算すると、(2.0*10^-8)mW (-77dB)になります。
これで、やっと距離D2を求められます。
受信側のトランシーバーのアンテナ利得は-2dBですから、アンテナ3から-75dBになる距離を求めます。
結果は障害物が無いとして約80mです。
障害物が無い所で2km届く受信能力があるトランシーバなら約300mになります。