距離計の作り方

この距離計は、非常に簡単ですが、測れる理由は数学です。
距離計そのものは、分度器をつけた板に筒を付け、垂直方向が分かるように錘を付けた糸を付けただけです。

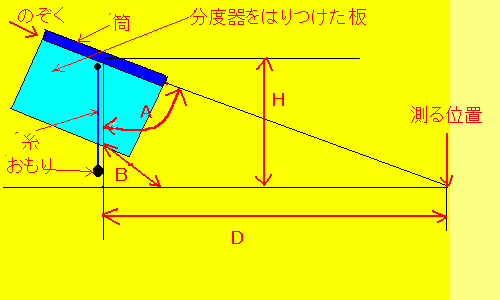
といっても、上図では分かりずらいと思いますが、原理が分かると納得できます。

地面にある石までの距離を知りたいとしましょう。
（１）まず、石を筒から覗きます。
　　　この時、視線とおもりを付けた糸が作る角度が上図の Ａ になります。
　　　上図の Ｈ は、目の高さとします。
　　　おもりを付けた糸の延長線は、地面に垂直で、これは、上図の Ｂ です。
　　　もう分かったと思います。
　　　分度器は上図の Ａ を測れるようにしておきます。

（２）距離を測る仕組みも分かったと思います。
　　１辺の長さと２つの角の大きさが分かれば、三角形は決まりますね。

（３）さて、どうやって三角形の１辺の長さ　Ｄ　を求めるかです。
　　高校生になると、三角関数というものを使って簡単に解けてしまいます。
　　三角関数を知らない場合は、実際に図を書いて解きます。
　　例えば、目の高さが１４０センチでしたら、１０分の１に縮めて１４センチの直線を書き、その一端に上図の角度 Ａ、もう一端に角度 Ｂ ９０度）を分度器でとって線を引きます。角度は１０分の１にはしません。
　　すると、引いた２本の線は交わって、三角形が出来ます。
　　求める辺の長さ　Ｄ　に対応するのは、目の高さの線（この場合１４センチの線）に直角な線です。
　　この線を定規で測ります。これが３０センチだとしたら、１０倍して３００センチ。石までは、３００センチと分かります。

（４）だいぶ面倒ですね。
　　　三角関数を使って求める式を書いておきます。
　　　ウィンドウズについている電卓で、簡単に計算できます。　　　
　　　D = H/tan(180-A-B)

このように、角度を利用して距離を測るのを、三角測量 と言います。
現在では、レーザで距離が測れますが、レーザ測量機が一般化するまでの長い間、測量はほとんどこの原理でした。
今回紹介したのは手持ちなのですが、手持ちですと、持ち方、姿勢により、図のＨの部分が変わってしまいますので、カメラ用の三脚に固定できるようにすると正確になります。
また、筒の部分（ここから目標を覗く）を小さな望遠鏡にし、角度を測る分度器の目盛りを、より細かく読みとるようにすると、より遠くまで測れます。
また、今までの説明は横にしても同じです。

＊レーザーを使っての測量は、測りたい地点に反射板を置き、その反射板に向けてレーザーを照射し、照射したレーザーと反射して戻ってきたレーザーの位相差から距離を求めます