棹ばかりの作り方
更新竿ばかりは、機械式の天秤の様に重さを測りたい物と重さが判っている分銅を比較する秤です。
最近は目にすることが少なくなったのでご存じない方が多いと思います。下図のようなものです。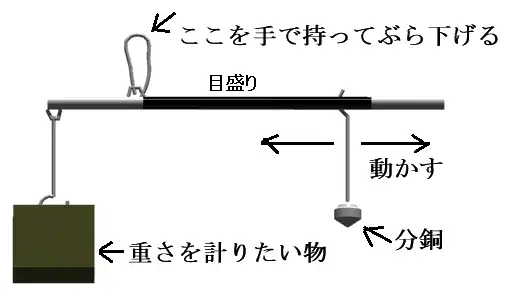
分銅を動かして棒(竿)を水平になるようにして分銅を下げている竿上の目盛りを読みます。構造が簡単で雑に扱っても壊れないので昔は行商人が使っていたようです。
構造は簡単なのですが、グラム単位まで計ろうとすると、なかなか大変です。
棹に質量が無いときの棹ばかりの計算
棹秤を作るために一つ一つ考えていきましょう
下図のように、測りたい物によって力$F_{1}$が生じ、分銅によって力$F_{2}$が生じます。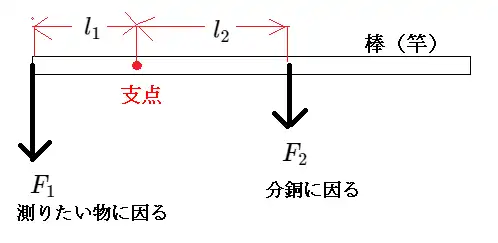
この2つの力は改めて言うまでもなく、それぞれの質量と重力加速度の積で、日常生活でいうところの重さです。
棒の質量をゼロとした場合、棒が水平で止まるためには、力$F_{1}$によって生じるモーメント$M_{1}$と力$F_{2}$によって生じるモーメント$M_{2}$の和がゼロになる必要があります。
$M_{1} = F_{1} l_{1} \tag{1} $ $M_{2} = - F_{2} l_{2} \tag{2} $ ただし、反時計回りを正、時計回りを負としています
棒が水平で停まるためには、$M_{1} + M_{2} = 0 $なので $ F_{1} l_{1} - F_{2} l_{2} = 0 \tag{3} $ ゆえに、棒の質量をゼロとしたときの$F_{1}$は $F_{1} =\frac{l_{1}}{l_{2}} F_{2} \tag{4}$
$M_{1} = F_{1} l_{1} \tag{1} $ $M_{2} = - F_{2} l_{2} \tag{2} $ ただし、反時計回りを正、時計回りを負としています
棒が水平で停まるためには、$M_{1} + M_{2} = 0 $なので $ F_{1} l_{1} - F_{2} l_{2} = 0 \tag{3} $ ゆえに、棒の質量をゼロとしたときの$F_{1}$は $F_{1} =\frac{l_{1}}{l_{2}} F_{2} \tag{4}$
棹に質量があるときの棹ばかりの計算
棒(竿)には質量があるので式4のようにはいきません。
棹秤を作るのに必要な力を書き出すと下図のようになります。
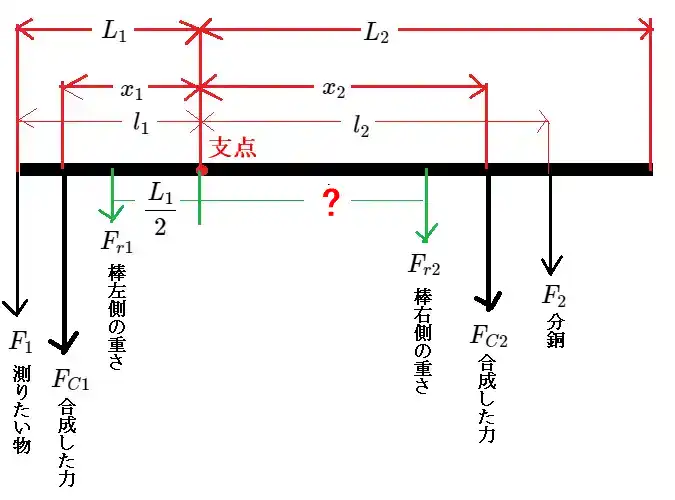
支点から左側は、左側の中点にある棒の重さから生じる力と、測りたい物から生じる力の合成した力$F_{C1}$となりますが、支点の右側が難しくて(図中の?が判りません)。
棹の重さが無視できるほど、測りたい物や分銅が重ければ、上記の棹の重さを無視した計算でよいのでしょうが、重い物を吊るときは棹は頑丈な物になり自然と重くなるので棹の重さを無視するのも気になります。
そこで、ChatGPとリートンに「棹秤の目盛りを刻む計算式を教えて」と訊ねました。
答えは、梃子の原理を表す超簡単な式と詳細は材質によって異なります云々。力学が得意な方なら解いてくれるか、解き方の説明ぐらいはしてくれるでしょう。 無料サービス版だからかわかりませんが、まだ、AIは使えません。
棹秤を作るのに必要な力を書き出すと下図のようになります。

支点から左側は、左側の中点にある棒の重さから生じる力と、測りたい物から生じる力の合成した力$F_{C1}$となりますが、支点の右側が難しくて(図中の?が判りません)。
棹の重さが無視できるほど、測りたい物や分銅が重ければ、上記の棹の重さを無視した計算でよいのでしょうが、重い物を吊るときは棹は頑丈な物になり自然と重くなるので棹の重さを無視するのも気になります。
そこで、ChatGPとリートンに「棹秤の目盛りを刻む計算式を教えて」と訊ねました。
答えは、梃子の原理を表す超簡単な式と詳細は材質によって異なります云々。力学が得意な方なら解いてくれるか、解き方の説明ぐらいはしてくれるでしょう。 無料サービス版だからかわかりませんが、まだ、AIは使えません。
平行な2つの力の合力の求め方
下図のような場合
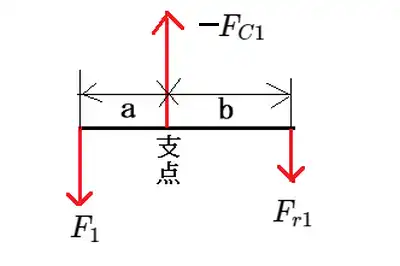
支点を回転軸にして回らないためには、モーメントの和がゼロになる必要があります。
$F_{1} a - F_{r1} b = 0 \tag{5}$ ゆえに $\frac{b}{a} =\frac{F_{1}}{F_{r1}} \tag{6}$ 式6から合力が作用する点が判ります。
合力の大きさと方向は、平行なベクトルなので足せばよいです。

支点を回転軸にして回らないためには、モーメントの和がゼロになる必要があります。
$F_{1} a - F_{r1} b = 0 \tag{5}$ ゆえに $\frac{b}{a} =\frac{F_{1}}{F_{r1}} \tag{6}$ 式6から合力が作用する点が判ります。
合力の大きさと方向は、平行なベクトルなので足せばよいです。
合成は、平行な2つの力の合力の計算で求め、この計算でこの力が作用する点$x_{1}$と$x_{2}$が求まります。 $F_{C1} x_{1} - F_{C2} x_{2} = 0 \tag{7} $ 式5が成り立つように分銅を動かせば、棹秤は水平で停止します。
計算は100円ショップで売っている簡単な電卓で出来ますが、ちょっと面倒です。
計算は100円ショップで売っている簡単な電卓で出来ますが、ちょっと面倒です。
棹秤の試作実験
手元にあった角棒を竿に、水を入れて重さを調整したペットボトルを分銅と測りたい物にして実験してみました。

2024年9月6日撮影
棹秤で測れる最小値は、測りたい物をぶら下げる方の棒の重さがあるので正確な値ではありませんが、目安としては分銅を吊り下げる方の棒の重さです。 この時、分銅なしでつり合います。

2024年9月6日撮影
棹秤で測れる最小値は、測りたい物をぶら下げる方の棒の重さがあるので正確な値ではありませんが、目安としては分銅を吊り下げる方の棒の重さです。 この時、分銅なしでつり合います。
計算して作るより、ペットボトルに水を入れて重さを調整し、実際にぶら下げて目盛りを付ける方が簡単に作れます。
長さ91cm、61gの角材を使い
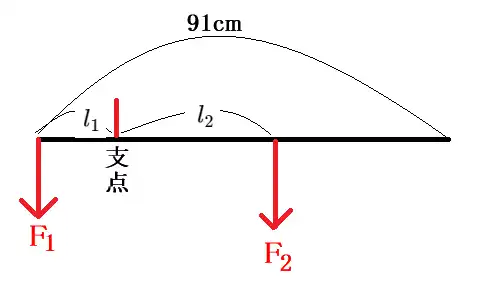
分銅代わりに水を入れて100gにしたペットボトルを下げ、測りたい物にも水を入れて、60g、100g、150g、200g、250g、300g、350g、400gに調整したペット下げ、
$l_{1}$は19cmに固定して$l_{2}$の長さを測ってみました。
$F_{2}=100gw$ $l_{1}= 19cm$
50g毎でも手間が掛かるのに10g毎に実測、と考えただけで気が遠くなります。
長さ91cm、61gの角材を使い

分銅代わりに水を入れて100gにしたペットボトルを下げ、測りたい物にも水を入れて、60g、100g、150g、200g、250g、300g、350g、400gに調整したペット下げ、
$l_{1}$は19cmに固定して$l_{2}$の長さを測ってみました。
$F_{2}=100gw$ $l_{1}= 19cm$
| $F_{1}$ | $l_{2}$ |
|---|---|
| 60gw | 分銅無 |
| 100gw | 4cm |
| 150gw | 12.5cm |
| 200gw | 23.5cm |
| 250gw | 29.0cm |
| 300gw | 38.0cm |
| 350gw | 46.0cm |
| 400gw | 53.0cm |