微分方程式解法入門 変数分離法
現代社会を支えているのは、微分方程式と言っても過言ではありません。
電気製品や構造物を始めとして殆どの物の設計製造は、微分方程式のお世話になっています。
微分方程式とは
傾きが$a$、$x=0$の$y$の値が$b$の直線 $y=ax+b$ を考えてみます。
この直線をX-Y座標で表すと、下図になります。
定数$a$と$b$の値によってこの直線は座標の何処にでも描くことが出来るので、右肩上がりで描いていますが、X軸やY軸に平行だったり、右肩下がりの直線にもなります。
この直線 $y=ax+b$ を$x$で微分すると
直線を含む曲線を表す式を微分すると、その点の接線を表す式になりますから、直線 $ax+b$ を微分したら傾きを表す$a$だけになるのは予想通りです。
式(1)こそが、最も簡単な微分方程式です。
そして、微分方程式を解くというのは、式(1)から元の$ax+b$ 求めることに他ならないということになります。
微分方程式 $\dfrac{dy}{dx}=a$ を解いてみましょう。解くと言っても、積分するだけです。
始めに掲げた直線の式は $ax+b$ でしたから、式(2)とbが定数Cに置き換わっています。X-Y座標上でこの直線を表すと、傾き$a$の直線に平行な直線になります。
定数$C$を $b$ に置き換えれば元の直線に戻りますが、微分方程式を解くと、元の直線にあった$b$ は定数 $C$ に含まれている値の1つということになってしまいます。
それで、微分方程式を解いて得た式(2)を一般解と言い、一般解の定数 $C$ を $b$ に置き換えて得た式を特殊解と言います。
実際は元の式が判らないですから(判って居たら微分方程式を解く必要は無い)、$x=0$のときは $y=b$ になる場合の式として積分定数 $C$ の値を $B$ と求めます。
ここで、少し実用的な例を考えてみましょう。
高い所から質量 $m$ のビー玉を落としたとき、ビー玉の落下速度はどうなるでしょう?
ただし、重力加速度を $g$、空気抵抗は無いとします。
ニュートンの運動方程式 $F=ma$ から始めます。
$F$は力、$m$ は質量、$a$ は加速度です。
加速度は、速度の微分で表せるので運動方程式は
ビー玉を落とした$0$ 秒での速度が $0$ という条件で式(6)の積分定数 $C$ は $0$ なので、ビー玉の落下速度は $v=-gt$ と求められました。
この直線をX-Y座標で表すと、下図になります。

定数$a$と$b$の値によってこの直線は座標の何処にでも描くことが出来るので、右肩上がりで描いていますが、X軸やY軸に平行だったり、右肩下がりの直線にもなります。
この直線 $y=ax+b$ を$x$で微分すると
$$\dfrac{dy}{dx}=a \tag{・・・式1}$$
となり、定数$a$だけになります。直線を含む曲線を表す式を微分すると、その点の接線を表す式になりますから、直線 $ax+b$ を微分したら傾きを表す$a$だけになるのは予想通りです。
式(1)こそが、最も簡単な微分方程式です。
そして、微分方程式を解くというのは、式(1)から元の$ax+b$ 求めることに他ならないということになります。
微分方程式 $\dfrac{dy}{dx}=a$ を解いてみましょう。解くと言っても、積分するだけです。
$$\displaystyle \int\frac{dy}{dx}dx=\displaystyle \int adx$$ $$=ax+C \tag{・・・式2}$$
ただし、$C$は定数(積分定数)です。始めに掲げた直線の式は $ax+b$ でしたから、式(2)とbが定数Cに置き換わっています。X-Y座標上でこの直線を表すと、傾き$a$の直線に平行な直線になります。
定数$C$を $b$ に置き換えれば元の直線に戻りますが、微分方程式を解くと、元の直線にあった$b$ は定数 $C$ に含まれている値の1つということになってしまいます。
それで、微分方程式を解いて得た式(2)を一般解と言い、一般解の定数 $C$ を $b$ に置き換えて得た式を特殊解と言います。
実際は元の式が判らないですから(判って居たら微分方程式を解く必要は無い)、$x=0$のときは $y=b$ になる場合の式として積分定数 $C$ の値を $B$ と求めます。
ここで、少し実用的な例を考えてみましょう。
高い所から質量 $m$ のビー玉を落としたとき、ビー玉の落下速度はどうなるでしょう?
ただし、重力加速度を $g$、空気抵抗は無いとします。
ニュートンの運動方程式 $F=ma$ から始めます。
$F$は力、$m$ は質量、$a$ は加速度です。
加速度は、速度の微分で表せるので運動方程式は
$$F=m\dfrac{dv}{dt} \tag{・・・式3}$$
落ちているビー玉には、上方を $+$ とすると $-mg$ という力 $F$ が働いているので、式(3)は $$m \dfrac{dv}{dt}=-mg \tag{・・・式(4)}$$
両辺を $m$ で割って $$\dfrac{dv}{dt}=-g \tag{・・・式(5)}$$
式(5)の微分方程式は簡単に解けます。 $$\displaystyle \int\frac{dv}{dt}dt=\displaystyle \int(-g)dt$$ $$v=-gt+C \tag{・・・式6}$$
ただし、$C$ は積分定数ビー玉を落とした$0$ 秒での速度が $0$ という条件で式(6)の積分定数 $C$ は $0$ なので、ビー玉の落下速度は $v=-gt$ と求められました。
変数分離法による微分方程式の解法
右辺に定数 $k$ と関数 $y$ がある微分方程式の解き方です。
右辺に含まれている関数 $y$ を求めるのですから大変そうです。前項の微分方程式の様に両辺を $x$ で積分することは出来ません、なぜなら $y$ は正体不明の関数だから。
そこで、$\dfrac{dy}{dx}=ky$ の両辺を $y$ で割り
積分公式を用いて
右辺に含まれている関数 $y$ を求めるのですから大変そうです。前項の微分方程式の様に両辺を $x$ で積分することは出来ません、なぜなら $y$ は正体不明の関数だから。
そこで、$\dfrac{dy}{dx}=ky$ の両辺を $y$ で割り
$$\displaystyle \frac{1}{y}\frac{dy}{dx}=k \tag{・・・式(7)}$$ $$\displaystyle \int\frac{1}{y}\frac{dy}{dx}dx=\int kdx \tag{・・・式(8)}$$ $$\displaystyle \int\frac{1}{y}dy=\int kdx \tag{・・・式(9)}$$
式(9)の左辺は $x$ の影響を受けず、右辺は $y$ の影響を受けないので分離されています。積分公式を用いて
$$ln(y)+C_{1}=kx+C_{2} \tag{・・・式(10)}$$ $$ln(y)=kx+C_{3} \tag{・・・式(11)}$$
対数指数の関係 $ ln(\alpha)=\beta$ $\alpha=e^{\beta}$ を用いて $$y=e^{kx+c^{3}}$$ $$y=e^{C^{3}}e^{kx}$$ $$y=Ce^{kx} \tag{・・・式(12)}$$
式(12)が一般解になります。$C$ は積分定数ですコンデンサーの放電を微分方程式で解く
上記の解き方が使える問題を解いてみましょう。
下図の左側の回路では充電してあるコンデンサーCとオフになっているスイッチ、抵抗Rが直列接続されています。
この回路でスイッチをオンにした時のコンデンサーに蓄えられていた電荷量Qの変化を求めたい、という問題です。
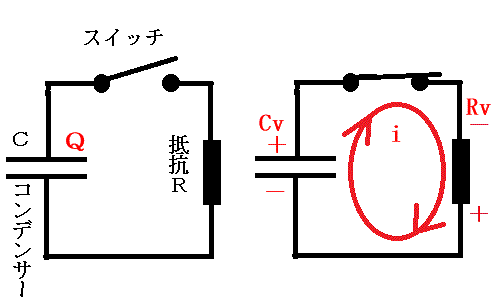
コンデンサーの容量は $C$、充電して溜まっている電荷量は $Q$、抵抗の値は $R$とします。
スイッチをオンにすると、回路内の電圧の和は $0$になるので
式(19)の両辺を $Q$で割ります。
次は、式(21)の様に右辺の関数yが二乗になっている場合ですが、両辺をyの自乗で割って、関数yを左辺に移し、右辺は定数kだけにして、積分公式を使って解きます。
右辺が関数yの自乗の微分方程式ですが、一般解は指数や対数も無い簡単な分数式です。
下図の左側の回路では充電してあるコンデンサーCとオフになっているスイッチ、抵抗Rが直列接続されています。
この回路でスイッチをオンにした時のコンデンサーに蓄えられていた電荷量Qの変化を求めたい、という問題です。

コンデンサーの容量は $C$、充電して溜まっている電荷量は $Q$、抵抗の値は $R$とします。
スイッチをオンにすると、回路内の電圧の和は $0$になるので
$$CC_{v}+R_{v}=0 \tag{・・・式(13)}$$
コンデンサーには、$Q$ = $C C_{v}$という関係あるので $$C_{v}=\displaystyle \frac{Q}{C} \tag{・・・式(14)}$$
抵抗の両端の電圧Rvは、オームの法則から $$R_{v}=iR \tag{・・・式(15)}$$ 回路を流れる電流 i は、コンデンサーに溜まっている電荷Qの時間的変化なので、 $$i=\displaystyle \frac{dQ}{dt} \tag{・・・式(16)}$$
式(13)に式(14)と式(15)を代入すると $$\displaystyle \frac{Q}{C}+iR=0 \tag{・・・式(17)}$$
式(17)の i を式(16)で置き換えると $$\displaystyle \frac{Q}{C}+\frac{dQ}{dt}R=0$$ $$\displaystyle \frac{Q}{C}=-\frac{dQ}{dt}R \tag{・・・式(18)}$$ $$\displaystyle \frac{dQ}{dt}=-\frac{1}{R}\frac{Q}{C} \tag{・・・式(19)}$$
式(19)は、先に解いた微分方程式 $\dfrac{dy}{dx}=ky$ と同じ形なので変数分離法で解きます。式(19)の両辺を $Q$で割ります。
$$\displaystyle \frac{dQ}{dt}=-\frac{1}{R}\frac{Q}{C} \tag{・・・式(19)}$$
変分離法を適用します $$\displaystyle \frac{1}{Q}\frac{dQ}{dt}=-\frac{1}{RC}$$ $$\displaystyle \int\frac{1}{Q}\frac{dQ}{dt}dt=-\int\frac{1}{RC}dt$$ $$\displaystyle \int\frac{1}{Q}dQ=-\int\frac{1}{RC}dt$$
積分公式を用いて $$ln(Q)+C_{1}=-\displaystyle \frac{1}{RC}t+C_{2}$$ $$ln(Q)=-\displaystyle \frac{1}{RC}t+C_{3}$$
対数指数公式を用いて $$Q=e^{(-\frac{1}{RC}t+C_{3})}$$ $$Q=e^{C_{3}}e^{-\frac{1}{RC}t}$$ $$Q=Ce^{-\frac{1}{RC}t} \tag{・・・式(20)}$$
求めた式(20)は一般解なので、 $t=0$ の時の電荷量 $Q$を与えて積分定数 $C$の値を求め、特殊解を得ます。次は、式(21)の様に右辺の関数yが二乗になっている場合ですが、両辺をyの自乗で割って、関数yを左辺に移し、右辺は定数kだけにして、積分公式を使って解きます。
$$\displaystyle \frac{dy}{dx}=ky^{2} \tag{・・・式(21)}$$
変数分離をするために両辺を $y^{2}$ で割ります。 $$\displaystyle \frac{1}{y^{2}}\frac{dy}{dx}=k$$ $$\displaystyle \int\frac{1}{y^{2}}\frac{dy}{dx}dx=\int kdx$$ $$\displaystyle \int\frac{1}{y^{2}}dy=\int kdx$$
積分公式を用いて $$-\displaystyle \frac{1}{y}+C_{1}=kx+C_{2}$$ $$y=\displaystyle \frac{1}{kx+C_{2}-C_{1}}$$ $$y=-\displaystyle \frac{1}{kx+C} \tag{・・・式(22)}$$
式(22)は微分方程式 式(21)の一般解です。$C$ は積分定数です。右辺が関数yの自乗の微分方程式ですが、一般解は指数や対数も無い簡単な分数式です。