微分方程式解法入門 非斉次微分方程式の解法
ここでいう斉次(または、同次)とは、未知関数と導関数の次数を揃えた式です。
微分方程式の解法で斎次式を取り上げるのは、「非斉次微分方程式の一般解は、その非斉次微分方程式の特殊解の1つと、 その非斉次微分方程式に対応する斉次微分方程式の一般解の和になる」という定理があるからです。
コンデンサーに電池を接続したときのコンデンサーに蓄えられる電荷量を求める
この定理を使って、コンデンサーに電源を繋いだ時の、コンデンサーに蓄えられる電荷$Q$と時間$t$の関係を導いてみましょう。
下記回路図で、スイッチを入れると、コンデンサーの電極間電圧$V_{c}$は$\dfrac{Q}{C}$、抵抗の電極間電圧$V_{R}$は$\dfrac{dQ}{dt}R$になります。 ただし、$Q$はコンデンサーに蓄えられている電荷量で、スイッチを入れる前は$Q=0$です。
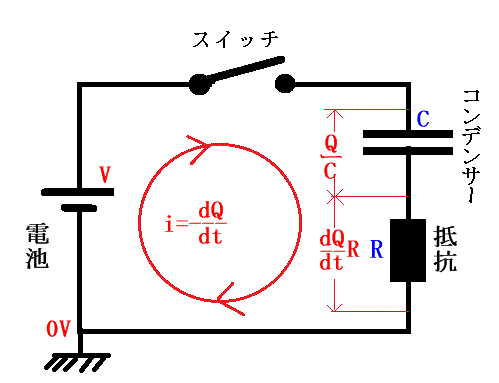
スイッチを入れると、抵抗の電極間電圧$V_{R}$とコンデンサーの電極間電圧$V_{c}$の和が電池の電極間電圧$V$に等しくなります。
抵抗の電極間電圧は、オームの法則から電流×抵抗値ですが、電流は電荷の時間当たりの変動量なので$\dfrac{dQ}{dt}R$になります。
そこで、$\displaystyle \frac{dQ}{dt}=0$の時の式3の特殊解を求めます。
式3は簡単になって
次に、非斉次微分方程式 式1に対応する斉次微分方程式 式5の一般解を求めます。
求めた解は、非斉次微分方程式 式1に対応する斉次微分方程式 式5の一般解なので、非斉次微分方程式 式1の特殊解式4を加えて非斉次微分方程式 式1の一般解式7が求められます。 下記回路図で、スイッチを入れると、コンデンサーの電極間電圧$V_{c}$は$\dfrac{Q}{C}$、抵抗の電極間電圧$V_{R}$は$\dfrac{dQ}{dt}R$になります。 ただし、$Q$はコンデンサーに蓄えられている電荷量で、スイッチを入れる前は$Q=0$です。

スイッチを入れると、抵抗の電極間電圧$V_{R}$とコンデンサーの電極間電圧$V_{c}$の和が電池の電極間電圧$V$に等しくなります。
$$V_{R}+V_{c}=V \tag{・・・式1}$$
コンデンサーの電極間電圧は、コンデンサーに蓄えられている電荷量$Q$とコンデンサーの容量$C$から$\dfrac{Q}{C}$抵抗の電極間電圧は、オームの法則から電流×抵抗値ですが、電流は電荷の時間当たりの変動量なので$\dfrac{dQ}{dt}R$になります。
$$R\displaystyle\frac{dQ}{dt}+\frac{Q}{C}=V\tag{・・・式2}$$
両辺を$R$で割ってちょっと整理 $$\displaystyle\frac{dQ}{dt}+\frac{1}{RC}Q=\frac{V}{R}\tag{・・・式3}$$
式3は$\dfrac{V}{R}=0$にすれば斉次微分方程式になるので、最初に記した定理が使えます。そこで、$\displaystyle \frac{dQ}{dt}=0$の時の式3の特殊解を求めます。
式3は簡単になって
$$\displaystyle \frac{1}{RC}Q=\frac{V}{R}$$ $$Q=CV \tag{・・・式4}$$
式4は式1の微分方程式の特殊解の一つです。ただし、$C$は積分定数では無くコンデンサーの容量です。次に、非斉次微分方程式 式1に対応する斉次微分方程式 式5の一般解を求めます。
$$\displaystyle\frac{dQ}{dt}+\frac{1}{RC}Q=0 \tag{・・・式5}$$
ここからは、変数分離法と積分公式、対数指数変換公式を用いて簡単に計算出来ます。 $$\displaystyle\frac{1}{Q}\frac{dQ}{dt}=-\frac{1}{RC}$$ $$\displaystyle\int\frac{1}{Q}\frac{dQ}{dt}dt=-\int\frac{1}{RC}dt$$
積分公式を用いて結果だけ拝借です。 $$ln(Q)+C_{1}=-\displaystyle\frac{1}{RC}t+C_{2}$$ $$ln(Q)=-\displaystyle \frac{1}{RC}t+C_{3}$$
指数対数変換の公式を用います。 $$Q=e^{(-\frac{1}{RC}t+C_{3})}$$ $$Q=e^{C_{3}}e^{(-\frac{1}{RC}t)}$$
$e^{C_{3}}$を$C_{4}$と置き換えて $$Q=C_{4}e^{-\frac{1}{RC}t} \tag{・・・式6}$$ $$Q=C_{4}e^{-\frac{1}{RC}t}+CV\tag{・・・式7}$$
ただし、$C_{4}$は積分定数、$C$はコンデンサーの容量です。求めた式7は一般解なので、$t=0$の時に$Q=0$という条件を式7に入れて積分定数$C_{4}$を求めます
$$0=C_{4}e^{-\frac{1}{RC}0}+CV$$ $$0=C_{4}+CV$$ $$C_{4}=-CV \tag{・・・式8}$$
積分定数$C_{4}$が求められたので一般解式7に代入して $$Q=-CVe^{-\frac{1}{RC}t}+CV\tag{・・・式9}$$ $$Q=CV(1-e^{-\frac{1}{RC}t})\tag{・・・式10}$$
コンデンサーに電池を繋いだ時のコンデンサーに蓄えられる電荷量と時間の関係が求められました。