微分方程式解法入門 単振り子の振動周期を求める
微分方程式を解いて単振り子の周期を求めてみます
単振り子というのは、紐などの一端に重りを付け、もう一方の端を固定してぶら下げたものです。
振り子の触れる角度が小さい時の周期は一定なので時計に使われていました(振り子時計)
単振り子の周期を求める微分方程式を組み立てるために下図を描きました。
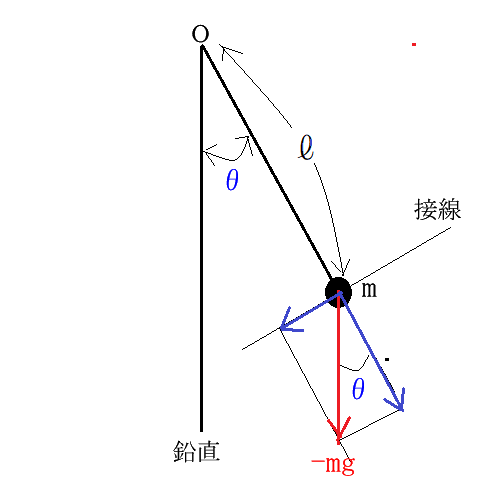
長さ$l$の紐の一端を$O$点に固定し、紐の他端に重り(質量$m$)を付けて単振り子を作ります。
計算の簡略化の為に重りには重力以外の力は働かないとします。$g$は単振り子が設置された場所の重力加速度です
先ず、単振り子が$θ$だけ振れている時の重りの加速度を考えます。
直線上の動きでしたら、距離$x$を時間$t$で微分して速度、速度を更に時間$t$で微分して加速度になります。
これと同じで、円周上の移動距離$lθ$を時間$t$で微分し更に時間$t$で微分します。
直線上の動きでしたら、距離$x$を時間$t$で微分して速度、速度を更に時間$t$で微分して加速度になります。
これと同じで、円周上の移動距離$lθ$を時間$t$で微分し更に時間$t$で微分します。
$$\dfrac{d^{2}lθ}{dt^{2}}$$
重りを振らせる力は重力の接線方向の力なので $$-mg\hspace{4pt}sinθ$$ 運動方程式は、 $$ml\dfrac{d^{2}lθ}{dt^{2}}=-mg\hspace{4pt}sinθ$$ 両辺を$ml$で割って $$\dfrac{d^{2}θ}{dt^{2}}=-\dfrac{g}{l}\hspace{4pt}sinθ$$
2階の微分方程式が出来ました。 振り子の振れ幅が極小さい場合は、$sinθ≒0$と考えてよいので
$$\dfrac{d^{2}θ}{dt^{2}}=-\dfrac{g}{l}\hspace{4pt}θ$$
計算しやすいように $$\omega^{2}=\dfrac{g}{l}$$
と置き換えます。この置き換えは振動を表している微分方程式解法の定石です。 $$\dfrac{d^{2}θ}{dt^{2}}=-\omega^{2}\hspace{4pt}θ\tag{1}$$
式1の両辺に$dθ/dt$を掛けて
$$\dfrac{dθ}{dt}\dfrac{d^{2}θ}{dt^{2}}=-\omega^{2}\hspace{4pt}θ\dfrac{dθ}{dt}\tag{2}$$
ここで、計算しやすいように $$\displaystyle{y}\prime\mathrm{{=}}\frac{dθ}{dt}\tag{3}$$ $$\dfrac{dy\prime}{dt}=\dfrac{d^{2}θ}{dt^{2}}\tag{4}$$
式2の左辺を式3と式4で置き換えると $$\dfrac{dy\prime}{dt}y\prime= -\omega^{2}θ\dfrac{dθ}{dt}\tag{5}$$
式5の左辺と右辺を$t$で積分して$y\prime$を元に戻すと $$\dfrac{1}{2} (\dfrac{dθ}{dt})^2 =-\dfrac{1}{2}\omega^{2}θ^{2}+C_{1}\tag{6}$$
ただし、$C_{1}$は積分定数です。 式6に、初期条件 時間$t=0$、$θ=θ_{0}$、速度$0$を設定して、積分定数$C_{1}$を求めます。
$$C_{1}=\dfrac{1}{2}\omega^{2}{θ_0}^{2}$$ これを式6に入れて $$\dfrac{1}{2} (\dfrac{dθ}{dt})^2 =-\dfrac{1}{2}\omega^{2}θ^{2}+\dfrac{1}{2}\omega^{2}{θ_0}^{2}\tag{7}$$ $$(\dfrac{dθ}{dt})^2 =\omega^{2}({θ_0}-θ^{2})\tag{8}$$
式8の両辺の平方根をとって $$\dfrac{dθ}{dt}=±\omega\sqrt({θ_0}-θ^{2})\tag{9}$$
式9は1階の微分方程式になり、解くために変数分離法を使います。 $$\dfrac{dθ}{\sqrt({θ_0}-θ^{2})}=±\omega dt\tag{10}$$
式10の両辺を積分しますが、左辺は複雑なので積分公式を使って $$sin^{-1}(\dfrac{θ}{θ_{0}})=±\omega t+C_{2}\tag{11}$$
ただし、$C_{2}$は積分定数です式11の右辺第1項は積分定数$C_{2}$との足し算なのでプラスマイナスどちらを選んでも同じなのでプラスを使います。 式11を$sin$で表すと、
$$\dfrac{θ}{θ_{0}}=sin(\omega t+C_{2})\tag{12}$$
三角関数の公式を使って式12の右辺を展開します。 $$\dfrac{θ}{θ_{0}}=sin(\omega t)cos(C_{2})+cos(\omega t)sin(C_{2})\tag{13}$$
初期条件は、$t=0$のときには$θ=θ_{0}$なので、式13に入れると$1=sin(C_{2})$なので式13は $$θ=θ_{0}cos(\omega t)\tag{14}$$ 求めたいのは単振り子の周期だったので、式14を見ると、余弦なので$\omega t$が$2π$毎に$θ$が元に戻ることが判ります。
そこで、$\omega t=2π$となり、単振り子の周期$T$は
式16を見て判るように、振れ幅の小さい単振り子の周期は、振り子が設置された場所の重力加速度と振り子の長さで決まります。
そこで、$\omega t=2π$となり、単振り子の周期$T$は
$$T=\dfrac{2π}{\omega}\tag{15}$$
$\omega^{2}=\dfrac{g}{l}$だったので、$\omega$を元に戻して $$T=\dfrac{2π}{\sqrt(\dfrac{g}{l})}$$ $$T=2π\sqrt(\dfrac{l}{g})\tag{16}$$
計算が長かったですが、振り子の長さ$l$の単振り子の周期$T$が求まりました。式16を見て判るように、振れ幅の小さい単振り子の周期は、振り子が設置された場所の重力加速度と振り子の長さで決まります。