微分と関数の曲線
時間の経過で変化するものがあるとき、グラフで表すことがあります。たとえば、停止している自動車や電車が動き出す時には時間が経つにつれて速度が上がりますが、 このような関係はY軸に速度、X軸を時間にして表すと解りやすいです。
$y=x^{2}$といった簡単な関数でもグラフにすると、$x$の変化で$y$が変化する様子が一目瞭然になります。人は視覚で考えた方が理解しやすいようです、 ただ、高等数学になるとイメージで捉えることが難しくなってしまうのが難点?
そこで、関数の微分をグラフに表して理解したいと思います。
$y=x^{2}$といった簡単な関数でもグラフにすると、$x$の変化で$y$が変化する様子が一目瞭然になります。人は視覚で考えた方が理解しやすいようです、 ただ、高等数学になるとイメージで捉えることが難しくなってしまうのが難点?
そこで、関数の微分をグラフに表して理解したいと思います。
微分係数とは
関数 $f(x)$ の平均変化率は
図の$α$の直線の傾きが$\frac{Δy}{Δx}$です
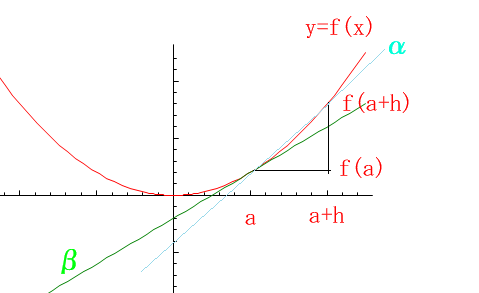
ここで、$h$ を限りなく $0$ に近づけて行ったときに、平均変化率が一定の値に限りなく近づくとき
関数$f(x)$ は、$x=a$ で微分可能であると言います。
地図の直線αが直線βに近づきます。この直線βは関数 $f(x)$ の接線になります。
そして、$h$ を限りなく$0$ に近づけたときの平均変化率の極限値を微分係数と言い、$f\prime(a)$で表します。
$$\dfrac{Δy}{Δx}=\frac{f(a+h)-f(a)}{(a+h)-a}=\dfrac{f(a+h)-f(a)}{h}$$
下図でイメージを掴んでください。図の$α$の直線の傾きが$\frac{Δy}{Δx}$です

ここで、$h$ を限りなく $0$ に近づけて行ったときに、平均変化率が一定の値に限りなく近づくとき
関数$f(x)$ は、$x=a$ で微分可能であると言います。
地図の直線αが直線βに近づきます。この直線βは関数 $f(x)$ の接線になります。
そして、$h$ を限りなく$0$ に近づけたときの平均変化率の極限値を微分係数と言い、$f\prime(a)$で表します。
$$f\prime(a)=\lim_{Δx\to0}\dfrac{Δy}{Δx}=\lim_{h\to0}\frac{f(a+h)-f(a)}{(a+h)-a}$$
接線の方程式を求める
直線の方程式は、$y=ax+b$ で表されます。
ただし、$a$ と $b$ は定数
ゆえに、点 $(x_{0}, y_{0})$を通り、かつ、傾きが $S$ の直線の方程式は
ただし、$a$ と $b$ は定数
ゆえに、点 $(x_{0}, y_{0})$を通り、かつ、傾きが $S$ の直線の方程式は
$$y_{0}=Sx_{0}+b$$ $$b=y_{0}-Sx_{0}$$
直線の方程式に$S$と$b$ を入れると $$y=Sx+y_{0}-Sx_{0}$$ $$y=S(x-x_{0})+y_{0}$$
点 $(a,f(a))$での関数 $f(x)$ の接線は、$S=f\prime(a)$、$x_{0}=a$、$y_{0}= f(a)$ なので、求める接線の方程式は $$y= f\prime(a)(x-a)+f(a)$$
例として、$f(x)=x^2$ の $x=1$ の$f(1)$ 上の接線の方程式を求めてみます。
微分係数 $f\prime(x)=2x$
$x=1$ での微分係数 $f\prime(1)=2$
$f(1)=1$
ゆえに、求める接線の方程式は $$y= 2(x-1)+1=2x-1$$
微分係数 $f\prime(x)=2x$
$x=1$ での微分係数 $f\prime(1)=2$
$f(1)=1$
ゆえに、求める接線の方程式は $$y= 2(x-1)+1=2x-1$$
導関数とは
微分係数を対応させる関数を導関数と言います。
すなわち、$f\prime(a)$ を求められる $f\prime(x)$ が導関数です。
$f(x)=x^2+1$
すなわち、$f\prime(a)$ を求められる $f\prime(x)$ が導関数です。
$$f\prime(x)=\lim_{Δx\to0}\dfrac{Δy}{Δx}=\lim_{h\to0}\frac{f(x+h)-f(x)}{(x+h)-x}$$
簡単な関数の導関数を求めてみましょう。$f(x)=x^2+1$
$$f\prime(x)=\lim_{h\to0}\frac{((x+h)^2+1)-(x^2+1)}{(x+h)-x}$$ $$=\lim_{h\to0}\frac{((x+h)^2+1)-(x^2+1)}{(x+h)-x}$$ $$=\lim_{h\to0}\frac{2hx+h^2}{h}=2x$$
微分するとは
関数 $f(x)$ の導関数を求めることを$f(x)$ を微分すると言います。微分して求めた導関数を更に微分することが出来ますが、2回微分とは言わずに2階微分と言います。
極大値、極小値、変曲点を求める
例として,$y=0$、1階微分 $y\prime=0$、2階微分 $y\prime\prime=0$ のときの$x$ が求めやすい
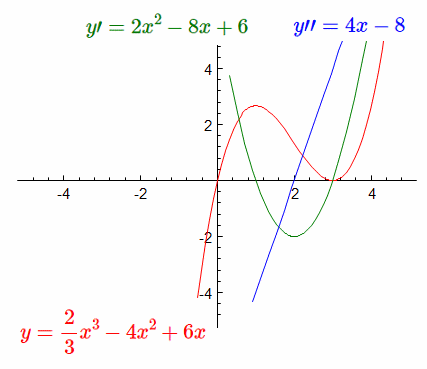
$$y=\dfrac{2}{3}x^{3}-4x^{2}+6x=\dfrac{2x(x-3)^{2}}{3}\tag{1}$$
で表される関数で説明します。式1を$x$で1階微分して $$y\prime=2x^{2}-8x+6=2(x-3)(x-1)\tag{2}$$
更に式2を$x$で微分して2階微分した $$y\prime\prime=4x-8=4(x-2)\tag{3}$$
をグラフで表したの下図です。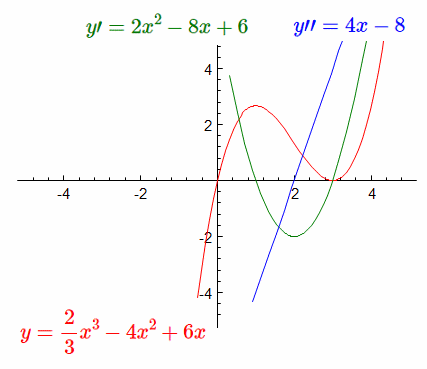
グラフを見ると一目瞭然です。
式1の極大値と極小値は、1階微分した $y\prime=2x^{2}-8x+6$ がX軸と交わる点にあります。
$y\prime=0=2x^{2}-8x+6$ として$x$ を求めると $x=1$ と $x=3$ が求まります。この $x$ を式1に代入して $y$ を求めると
$x=1$ $y=\dfrac{8}{3}$ 、$x=3$ $y=0$ となりますから、 極大値は$(1,\dfrac{8}{3})$、極小値は$(3,0)$ となります。
上凸から下凸に変わる点または下凸から上凸に変わる点を変曲点と言いますが、 変曲点は2階微分した$y\prime\prime=4x-8$ の符号が変わる点なのでX軸と交わる $x=2$ を $y=\dfrac{2}{3}x^{3}-4x^{2}+6x$ に代入して $y=\dfrac{4}{3}$
変曲点は$(2,\dfrac{4}{3})$
式1の極大値と極小値は、1階微分した $y\prime=2x^{2}-8x+6$ がX軸と交わる点にあります。
$y\prime=0=2x^{2}-8x+6$ として$x$ を求めると $x=1$ と $x=3$ が求まります。この $x$ を式1に代入して $y$ を求めると
$x=1$ $y=\dfrac{8}{3}$ 、$x=3$ $y=0$ となりますから、 極大値は$(1,\dfrac{8}{3})$、極小値は$(3,0)$ となります。
上凸から下凸に変わる点または下凸から上凸に変わる点を変曲点と言いますが、 変曲点は2階微分した$y\prime\prime=4x-8$ の符号が変わる点なのでX軸と交わる $x=2$ を $y=\dfrac{2}{3}x^{3}-4x^{2}+6x$ に代入して $y=\dfrac{4}{3}$
変曲点は$(2,\dfrac{4}{3})$