2次方程式の解き方
2次方程式とは、$ax^2+bx+c=0$ ただし、$a,b,c$ は定数
というもので、この方程式をみたす $x$ を求めることを2次方程式の解くと言います
ここでは$x$ が2乗ですが、n乗の方程式は、重複解を含んでN個の複素数解を持ちます。
複素数というのは、$a+ib$ で表され、$i$ の二乗が$-1$ になります(ただし、$a,b$ は定数)
ですから、$ax^2+bx+c=0$ の解は重複を含めて2個あります
例として、$f(x)=2x^2-7x+4$ をグラフに表すと
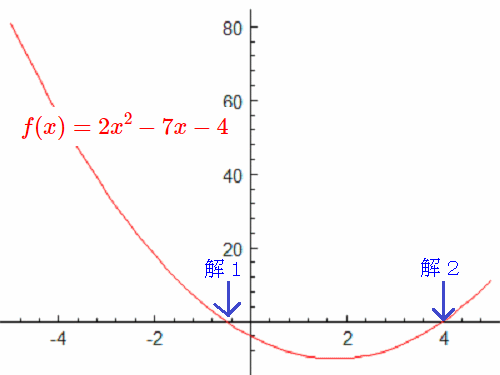
$f(x)=2x^2-7x-4=0$ ですから、解は$y=0$ になる$x$ の図中の解1と解2になります
というもので、この方程式をみたす $x$ を求めることを2次方程式の解くと言います
ここでは$x$ が2乗ですが、n乗の方程式は、重複解を含んでN個の複素数解を持ちます。
複素数というのは、$a+ib$ で表され、$i$ の二乗が$-1$ になります(ただし、$a,b$ は定数)
ですから、$ax^2+bx+c=0$ の解は重複を含めて2個あります
例として、$f(x)=2x^2-7x+4$ をグラフに表すと

$f(x)=2x^2-7x-4=0$ ですから、解は$y=0$ になる$x$ の図中の解1と解2になります
解の公式を使って2次方程式を解く
2次方程式の解の公式
$2x^2-7x+4=0$ の解でしたら、$a=2,b=-7,c=4$を解の公式に代入し
$$x=\dfrac{-b\pm{\sqrt{b^2-4ac}}}{2a}$$
は、2次方程式の解法には万能です。数値を入れれば機械的に答えが求まります。$2x^2-7x+4=0$ の解でしたら、$a=2,b=-7,c=4$を解の公式に代入し
$$x=\dfrac{-(-7)\pm{\sqrt{(-7)^2-(4\times 2 \times -4)}}}{2\times 2}$$
$$=\dfrac{7\pm9}{4}$$ ゆえに、$x=4$ と $x=- \dfrac{1}{2}$ 2次方程式の解の判別式
2次方程式 $ax^2+bx+c=0$ を解く「解の公式」の平方根内の計算式
$b^2-4ac$
を「二次方程式の解の判別式」と言います。
$D=b^2-4ac >0$ なら実数解を2つ持ちます
$D=b^2-4ac=0$ なら重複した実数解を持ちます
$D=b^2-4ac <0$ なら複素数解または虚数解を持ちます
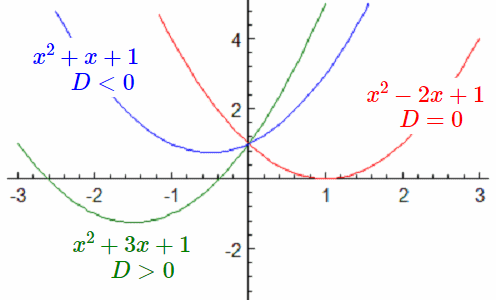
下のグラフは、判別式の違いによる例です
$x^2+3x+1$ $D>0$
$x^2-2x+1$ $D=0$
$x^2+x+1$ $D<0$
$b^2-4ac$
を「二次方程式の解の判別式」と言います。
$D=b^2-4ac >0$ なら実数解を2つ持ちます
$D=b^2-4ac=0$ なら重複した実数解を持ちます
$D=b^2-4ac <0$ なら複素数解または虚数解を持ちます
下のグラフは、判別式の違いによる例です
$x^2+3x+1$ $D>0$
$x^2-2x+1$ $D=0$
$x^2+x+1$ $D<0$

因数分解して2次方程式を解く
この方法は、因数分解出来れば3次以上の方程式も解ける方法ですが、因数分解するという問題になってしまいます。
$2x^2-7x-4=0$ の場合は、
$(2x+1)(x-4)=0$
となるので、左辺を$0$ にする$x=4$ と $x=- \dfrac{1}{2}$ が解です。
因数分解が苦手な方には不向きな方法ですが、3次方程式を解く場合には1つでも因数が見つかれば、 あとは二次方程式になるので解の公式を使って求められます。
$2x^2-7x-4=0$ の場合は、
$(2x+1)(x-4)=0$
となるので、左辺を$0$ にする$x=4$ と $x=- \dfrac{1}{2}$ が解です。
因数分解が苦手な方には不向きな方法ですが、3次方程式を解く場合には1つでも因数が見つかれば、 あとは二次方程式になるので解の公式を使って求められます。
平方完成で2次方程式を解く
平方完成というのは、左辺を強引に二乗にして両辺の平方根をとって解を求める手法なのですが、2次方程式の解の公式を導いているだけです。
左辺を変数を含む平方の式に、右辺を定数だけの式に変形するのが平方完成です。
式4の左辺から $x$ を含まない部分を右辺に移動して
$x$ を求めるために式5の両辺の平方根をとります。
ですから、平方完成で解くと求められない限り、2次方程式の解の公式を使う方が早いです。
左辺を変数を含む平方の式に、右辺を定数だけの式に変形するのが平方完成です。
$$ax^2+bx+c=0 \tag{1}$$
先ず、定数$c$ を右辺に移動します。 $$ax^2+bx=-c \tag{2}$$
式2の両辺を$a$ で割ります。 $$x^2+\dfrac{b}{a}x=-\dfrac{c}{a} \tag{3}$$
左辺を $x$ を含む平方の式に変形します。 $$(x+\dfrac{b}{2a})^2-\dfrac{b^2}{4a^2}= -\dfrac{c}{a} \tag{4}$$
式4の $x$ を含む()の二乗を展開すると $$(x+\dfrac{b}{2a})^2= x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}$$
となるので、式4では$\dfrac{b^2}{4a^2}$ を引いています。式4の左辺から $x$ を含まない部分を右辺に移動して
$$(x+\dfrac{b}{2a})^2= \dfrac{b^2}{4a^2}-\dfrac{c}{a} \tag{5}$$
これで、平方完成になりました。$x$ を求めるために式5の両辺の平方根をとります。
$$x+\dfrac{b}{2a}= \pm{\sqrt{ \dfrac{b^2}{4a^2}-\dfrac{c}{a}}} \tag{6}$$ $$x= -\dfrac{b}{2a}\pm{\sqrt{ \dfrac{b^2}{4a^2}-\dfrac{c}{a}}} \tag{7}$$
式7を整理します。 $$x= -\dfrac{b}{2a}\pm{\sqrt{ \dfrac{b^2-4ac}{4a^2}}} \tag{8}$$ $$x= -\dfrac{b}{2a}\pm{\dfrac{\sqrt{b^2-4ac}}{2a}} \tag{9}$$ $$x= \dfrac{-b\pm{\sqrt{b^2-4ac}}}{2a}\tag{10}$$
式10は、2次方程式の解の公式です。ですから、平方完成で解くと求められない限り、2次方程式の解の公式を使う方が早いです。