3次方程式の解き方
2次方程式 $ax^2+bx+c$ は、解の公式
「カルダノの公式」という3次方程式の一般解を求めるものがあります。規則性がある公式ですが、私にはとても憶えられません。
$$x= \dfrac{-b\pm{\sqrt{b^2-4ac}}}{2a}\tag{1}$$
で容易に求められますが、3次方程式にはこんな便利な公式はありません。「カルダノの公式」という3次方程式の一般解を求めるものがあります。規則性がある公式ですが、私にはとても憶えられません。
「カルダノの公式」
$$ax^3+bx^2+cx+d=0$$
ただし、 $a\neq 0$の一般解は \begin{eqnarray} x= \begin{cases} -\dfrac{b}{3a}+\sqrt[3]{-\dfrac{q}{2}+\sqrt{(\dfrac{q}{2})^2+(\dfrac{p}{3})^3} }+\sqrt[3]{-\dfrac{q}{2}-\sqrt{(\dfrac{q}{2})^2+(\dfrac{p}{3})^3} }\\ -\dfrac{b}{3a}+\omega^3\sqrt[3]{-\dfrac{q}{2}+\sqrt{(\dfrac{q}{2})^2+(\dfrac{p}{3})^3} }+\omega^2\sqrt[3]{-\dfrac{q}{2}-\sqrt{(\dfrac{q}{2})^2+(\dfrac{p}{3})^3} }\\ -\dfrac{b}{3a}+\omega^2\sqrt[3]{-\dfrac{q}{2}+\sqrt{(\dfrac{q}{2})^2+(\dfrac{p}{3})^3} }+\omega^3\sqrt[3]{-\dfrac{q}{2}-\sqrt{(\dfrac{q}{2})^2+(\dfrac{p}{3})^3} }\\ \end{cases} \end{eqnarray}
ただし、
$$p=\dfrac{c}{a}-{1}{3}(\dfrac{b}{a})^2$$ $$q=\dfrac{d}{a}-\dfrac{1}{3}\dfrac{b}{a}\dfrac{c}{a}+\dfrac{2}{27}(\dfrac{b}{a})^2$$ $$\omega^2=-\dfrac{1+\sqrt{3}i}{2}$$ $$\omega^3=1$$
因数分解して次数を下げる方法
N次方程式
ただし、私たちは、因数分解と言えば、有理数(分数で表すことが出来る数)か、深く考えても、 無理数(平方根で表される数、円周率、自然対数など)を含めての範囲でしか考えませんね。 工学計算では複素数が表れることが多いで、複素数を含めての因数分解がありますが。
3次方程式で因数が1つ見つかれば、あとは2次方程式になるので、重複解を含めて3個の解が容易に求められます。
たとえば、
$x=-\frac{1}{2}$は重複解(重根)です。
実は、この3次方程式は
グラフに表すと
$$a_{n}x^{n}+a_{n-1}x^{n-1}+・・・・・+a_{1}x^{1}+a_{0}x^{0}=0$$
は、複素数まで範囲を広げると必ず因数分解出来ます。(ガウスによって因数分解出来ることが証明されています)ただし、私たちは、因数分解と言えば、有理数(分数で表すことが出来る数)か、深く考えても、 無理数(平方根で表される数、円周率、自然対数など)を含めての範囲でしか考えませんね。 工学計算では複素数が表れることが多いで、複素数を含めての因数分解がありますが。
3次方程式で因数が1つ見つかれば、あとは2次方程式になるので、重複解を含めて3個の解が容易に求められます。
たとえば、
$$2x^3+4x^2+\dfrac{5}{2}x+\dfrac{1}{2}=0$$
この一見難しそうな3次方程式は、因数として-1が見つかれば $$(x+1)(2x^2+2x+\dfrac{1}{2})=0$$ 2次方程式部分は、2次方程式の解の公式(上記 式1)を使って $$x=\dfrac{-2\pm{\sqrt{2^2-4\times 2 \times \frac{1}{2}}}}{2\times 2}= -\dfrac{1}{2}$$
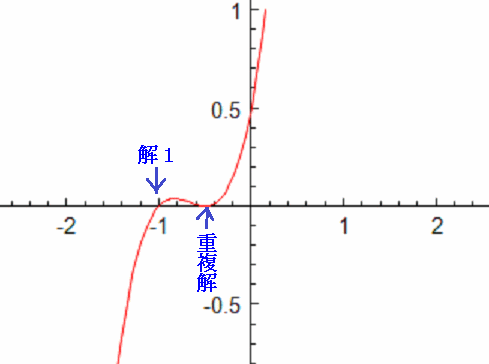
ゆえに解は、$x=-\frac{1}{2}$ と $x=-1$$x=-\frac{1}{2}$は重複解(重根)です。
実は、この3次方程式は
$$(x+\dfrac{1}{2})(2x+1)(x+1)=0$$
と完全に因数分解出来ます。グラフに表すと

4次方程式では、$x^2=t$ と置いて2次方程式に変換して解く方法が使えることがありますが、3次方程式以上になると、 紙の上で鉛筆を動かしただけでは解けないものが殆どです。
逆に言えば、試験で3次以上の方程式の出題があったときには、因数分解や変数の置き換え($x^2=t$)などで解ける方程式ということです。
3次方程式の係数と解の関係
ところで、3次方程式は、式2の右辺の様に因数分解出来ます。
$$ax^3+bx^2+cx+d=a(x-α)(x-β)(x-γ)\tag{2}$$
そこで、式2の右辺を展開します。 $$a(x-\alpha)(x-\beta)(x-\gamma)=ax^3-a(\alpha+\beta+\gamma)x^2+a(\alpha\beta+\alpha\gamma+\beta\gamma)x+a\alpha\beta\gamma\tag{3}$$
式2の左辺と式3の右辺は等しいですから、次数が同じ$x$の係数も等しいので $$b=-a(\alpha+\beta+\gamma)\tag{4}$$ $$c=a(\alpha\beta+\alpha\gamma+\beta\gamma)\tag{5}$$ $$d=a\alpha\beta\gamma\tag{6}$$
元の3次方程式の係数$a,b,c,d$ を左辺に移動して $$\dfrac{b}{a}=-(\alpha+\beta+\gamma)\tag{7}$$ $$\dfrac{c}{a}=(\alpha\beta+\alpha\gamma+\beta\gamma)\tag{8}$$ $$\dfrac{d}{a}=\alpha\beta\gamma\tag{9}$$
$\alpha.\beta.\gamma$ は、方程式 $ax^3+bx^2+cx+d=0$ の解です