虚数解を持つ方程式
3次以上の方程式は鉛筆を持ってで解けないものが多く、試験問題では学習レベルに応じて解ける範囲で作成されます。 たとえば、整数や無理数の範囲、有理数を含む範囲、虚数まで含む範囲で解ける。因数分解で解ける。などのようにです。
このページでは、虚数解が与えられた問題を考えてみます。
これは、「実数を係数に持つ高次方程式が虚数解 $\alpha$ を持つときには、 その共役複素数 $\overline{\alpha}$ も解である($a+bi$ という解を持つ方程式は、 $a-bi$ という解を持つ。ただし、$a$,$b$ は実数)」ということを利用して解く問題です。
虚数というのは、自乗して-1になるという理解し難い数で、$i$ で表します。
$i^2=-1$ です。
物理や工学では電流を表すときに $i$ を使うので虚数は $j$ で表し、数学以上に意味のある数として実感出来ます。
このページでは、虚数解が与えられた問題を考えてみます。
これは、「実数を係数に持つ高次方程式が虚数解 $\alpha$ を持つときには、 その共役複素数 $\overline{\alpha}$ も解である($a+bi$ という解を持つ方程式は、 $a-bi$ という解を持つ。ただし、$a$,$b$ は実数)」ということを利用して解く問題です。
虚数というのは、自乗して-1になるという理解し難い数で、$i$ で表します。
$i^2=-1$ です。
物理や工学では電流を表すときに $i$ を使うので虚数は $j$ で表し、数学以上に意味のある数として実感出来ます。
$x^2-2x+5=0$ という方程式を、二次方程式の解の公式で解いてみます。
2次方程式の解の公式というのは、$ax^2+bx+c=0$ という2次方程式の解 $x$ は
$a=1$ $b=-2$ $c=5$ なので、解の公式に代入して
2次方程式なので解は2つで、共役複素数になっています。
一見簡単そうに見えた2次方程式ですが、虚数を知らないと解けません。
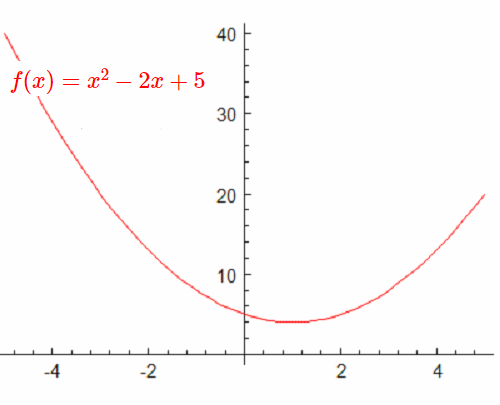
一般的な座標系でグラフに表すと "y=0" の点がありません。関数 $f(x)$ のグラフを描いて関数の曲線が X軸に接しているかX軸との交点を持つときには、関数 $f(x)$ は実数解を持ちます。
この2次方程式は、実数を係数に持つ高次方程式が虚数解 $\alpha$ を持つときには、 その共役複素数 $\overline{\alpha}$ も解である」から、 複素数 $a+bi$ を解に持つ2次方程式は、その共役複素数を解に持つの
$$\{x-(a+bi)\}\{x-(a-bi)\}$$ $$=x^2-2ax-(a^2+b^2) \tag{式2}$$ という式から作っただけです。
ですから、虚数解を1つ与えられれば2次方程式は作れますし、任意の虚数解を持つ2次方程式も式2から作れます。
2次方程式の解の公式というのは、$ax^2+bx+c=0$ という2次方程式の解 $x$ は
$$x= \dfrac{-b\pm{\sqrt{b^2-4ac}}}{2a}\tag{1}$$
というものです。$a=1$ $b=-2$ $c=5$ なので、解の公式に代入して
$$x=\dfrac{-(2)\pm{\sqrt{(-2)^2-4\times{1}\times{5}}}}{2\times{1}}$$ $$=\dfrac{-2\pm{\sqrt{-16}}}{2}$$ $$=\dfrac{-2\pm{4i}}{2}$$ $$=1\pm{2}i$$
ゆえに、2次方程式 $x^2-2x+5=0$ の解は、$x=1+2i$ と $x=1-2i$ になります。2次方程式なので解は2つで、共役複素数になっています。
一見簡単そうに見えた2次方程式ですが、虚数を知らないと解けません。
一般的な座標系でグラフに表すと "y=0" の点がありません。関数 $f(x)$ のグラフを描いて関数の曲線が X軸に接しているかX軸との交点を持つときには、関数 $f(x)$ は実数解を持ちます。

この2次方程式は、実数を係数に持つ高次方程式が虚数解 $\alpha$ を持つときには、 その共役複素数 $\overline{\alpha}$ も解である」から、 複素数 $a+bi$ を解に持つ2次方程式は、その共役複素数を解に持つの
$$\{x-(a+bi)\}\{x-(a-bi)\}$$ $$=x^2-2ax-(a^2+b^2) \tag{式2}$$ という式から作っただけです。
ですから、虚数解を1つ与えられれば2次方程式は作れますし、任意の虚数解を持つ2次方程式も式2から作れます。
3次方程式と虚数解
3次方程式は重複解を含めて解は3つありますから、 虚数解を1つ提示されたらその虚数解の共役複素数の解で作った2次式で問題の3次式を割れば、ヒントが得られます。
たとえば、$1+2i$ が解の1つである3次方程式は、重複解を含めて解が3つあるので
$a=-(2+\beta)$
$b=5+2\beta$
$c=-5\beta$
このようにすれば、任意の虚数解を含む3つの解を持つ3次方程式が作れます。
たとえば、$1+2i$ が解の1つである3次方程式は、重複解を含めて解が3つあるので
$(x-\beta)\{x-(1+2i)\}\{x-(1-2i)\}$
$=x^3-(2+\beta)x^2+(5+2\beta)x-5\beta$ ・・・式3
式3が $x^3+ax^2+bx+c$ に等しいので、$=x^3-(2+\beta)x^2+(5+2\beta)x-5\beta$ ・・・式3
$a=-(2+\beta)$
$b=5+2\beta$
$c=-5\beta$
このようにすれば、任意の虚数解を含む3つの解を持つ3次方程式が作れます。