多項式の割り算・余剰定理と因数分解
小学校の算数に、たとえば「41を5で割ると、商が8で余りが1」という計算があります。
整数 $a,b,c,d$ で表すと $a\div b=c,,,d$
商が $c$ 余りが $d$
この様な割り算は $a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x^{1}+a_{0}x^{0}$ の多項式でも出来ます。
割られる文字式の文字変数の一番大きな次数が割る文字式の一番大きい次数以下になるまで割って行きます。
例として、 $2x^2+4x+3$ を $x+1$ で割ってみます。
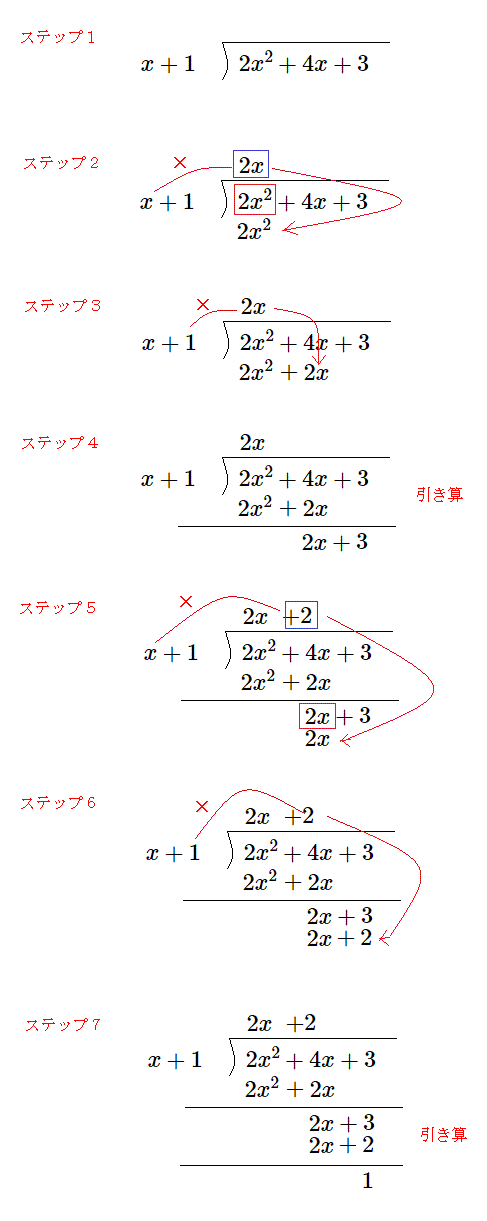
- ステップ1:割る文字式と割られる文字式をノートに書きます。
- ステップ2:割られる文字式 $2x^2+4x+3$ の中で一番大きな次数(赤い四角の中)の $2x^2$ を消す方法を考えます。
それには、割る文字式 $x+1$ で次数が一番大きい $x$ にある文字数を掛けて $2x^2$ になればよいので、 青い四角の位置に $2x$、赤い四角の下に $2x^2$ と書きます。 - ステップ3:割る数の定数 $1$ とステップ2の青い四角の位置に書いた $2x$ を掛けて $2x$ の右に書きます。
- ステップ4:割られる文字式 $2x^2+4x+3$ からステップ3で出て来た文字式 $2x^2+2x$ を引いてその下に書きます
- ステップ5:ステップ4引いた残り $2x+3$ に対して、ステップ2からの操作をします
- ステップ7:$2x^2+4x+3$ を $x+1$ で割ると、商は $2x+2$ 、あまりは $1$ となります。

多項式同士の割り算と言っても小学校以来慣れ親しんで来た整数同士の割り算を筆算でするのと変わりありません。 数では位を合わせましたが、多項式では次数を合わせるだけです。
余剰定理を利用して因数分解する
上記で多項式の割り算の説明に用いた $f(x)=2x^2+4x+3$ ですが、余剰定理によって $x+1$ で割った余りは、
$x+1=0$ として $x=-1$ この $-1$ を $f(x)=2x^2+4x+3$ に入れて
多項式 $f(x)=3x^3+12x^2+15x+6$ に $x+2$ で割った余りは余剰定理によって
余りが $0$ なら割る文字式で因数分解出来ます。因数分解出来れば、3次方程式なら次数が1つ下がるので2次方程式の解の公式を使えます。
$x+1=0$ として $x=-1$ この $-1$ を $f(x)=2x^2+4x+3$ に入れて
$$f(-1)=2\times(-1)^2+4\times(-1)+3=1$$
と、割り算をしないで余りが求められました。多項式 $f(x)=3x^3+12x^2+15x+6$ に $x+2$ で割った余りは余剰定理によって
$$f(-2)=3\times (-2)^3+12\times(-2)^2+15\times(-2)+6=0$$
ゆえに、多項式 $f(x)=3x^3+12x^2+15x+6$ は $x+2$ で割り切れるから $f(x)=3x^3+12x^2+15x+6$
$=(x+2)(3x^3+6x+3)$
$=3(x+2)(x^2+2x+1)$
$=3(x+2)(x+1)^2$
多項式を1次式で割った余りは、余剰定理によって割り算をしないでも余りが求められます。$=(x+2)(3x^3+6x+3)$
$=3(x+2)(x^2+2x+1)$
$=3(x+2)(x+1)^2$
余りが $0$ なら割る文字式で因数分解出来ます。因数分解出来れば、3次方程式なら次数が1つ下がるので2次方程式の解の公式を使えます。