*数式が多いために正常に表示されるまで時間が掛かる場合があります。
三角関数- 正弦定理の使い方 距離を測る
最も解りやすい三角関数の使い方は、遠くの点までの距離を測る問題(三角測量)だと思います。
下記図において、$A$ 点から $D$ 点までの距離 $x$ を求めることにします。
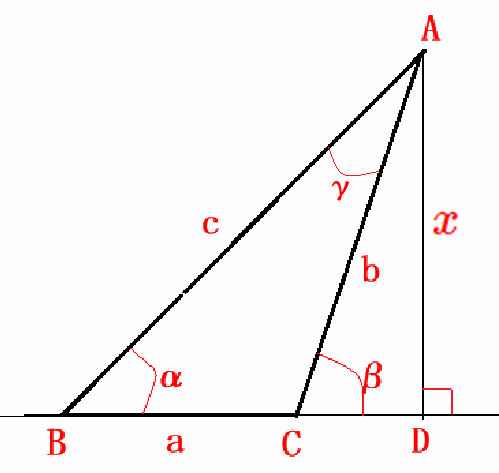
測量して判明しているのは。辺aの長さと∠ABCの角度α、∠ACDの角度βです
正弦定理によると、∠ABCの角度αと辺b、∠BACの角度と辺aの間には次の関係があります。
現在の測量では、レーザーを使った距離測定を行っているので、角度を測るのでは無くて三角形の辺の長さから求めています
下記図において、$A$ 点から $D$ 点までの距離 $x$ を求めることにします。

測量して判明しているのは。辺aの長さと∠ABCの角度α、∠ACDの角度βです
正弦定理によると、∠ABCの角度αと辺b、∠BACの角度と辺aの間には次の関係があります。
$$\dfrac{b}{\sin{\alpha}}=\dfrac{a}{\sin{\gamma}}\tag{1}$$
角度 $\gamma$ は三角形の内角の和が $\pi$ であることから $$\pi=\gamma+\alpha+(\pi-\beta)$$ $$\gamma=\beta-\alpha$$ 式1から辺bは $$b=a\dfrac{\sin\alpha}{\sin\gamma}$$ 求めたい $x$ は $$x=b\sin\beta=a\dfrac{\sin{\beta}\sin{\alpha}}{\sin{\gamma}}$$
よって求めたい $x$ は、角度 $\gamma$ を戻して $$x=a\dfrac{\sin{\beta}\sin{\alpha}}{\sin{(\beta-\alpha)}}$$
現在の測量では、レーザーを使った距離測定を行っているので、角度を測るのでは無くて三角形の辺の長さから求めています
正弦定理の説明
上記では、三角測量で三角形の正弦定理を使った求め方を説明しましたが、 正弦定理には、三角形の外接円の直径が辺の長さとその辺が対応する角度のsinの比に等しいという性質があります。
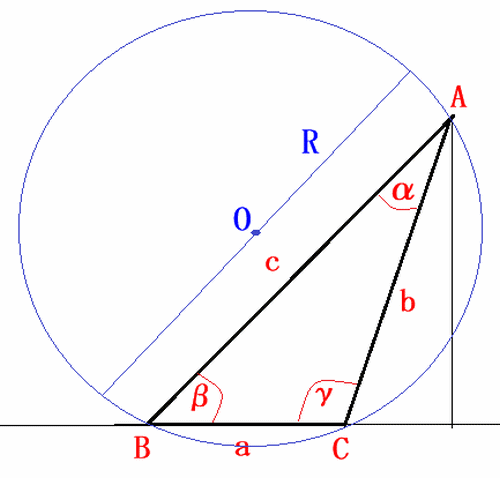
上図の三角形ABCが外接する円の半径 $R$ の2倍の直径とには次の関係があります。

上図の三角形ABCが外接する円の半径 $R$ の2倍の直径とには次の関係があります。
$$\dfrac{a}{\sin{\alpha}}=\dfrac{b}{\sin{\beta}}=\dfrac{c}{\sin{\gamma}}=2R\tag{2}$$