*数式が多いために正常に表示されるまで時間が掛かる場合があります
ベクトルと一次従属と一次独立
ベクトルとは、大きさに働く方向が加わったものです。
速度や加速度はベクトルですが、方向性が無い時間はベクトルではありません。
ベクトルを図で表示する場合は下図の様に矢印で表し、矢印の元を始点、矢印の先を終点、矢印の長さ部分を有向線分と言います。
ただし、ベクトルでは、始点の位置には関係無く、矢印の向きと長さだけが重要です。 ですから、大きさが等しくて向きが同じ平行なベクトルは同一です。並行で向きが逆なら-符号を付けます。$\vec{a}=-\vec{a}$
(ベクトルはゴシック体で表しますが、間違えやすいので→を付けています)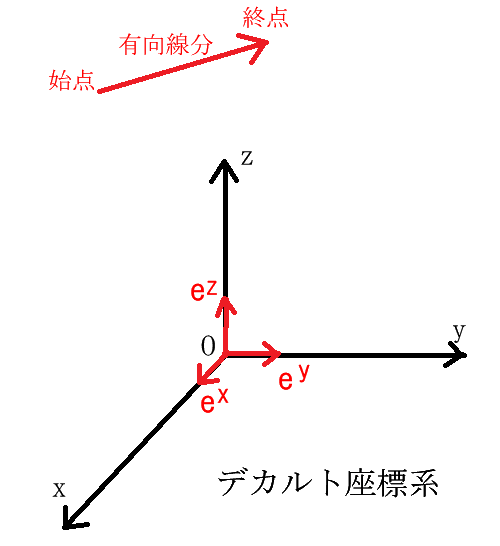
原点を0とする直交座標系で、x、y、z方向に単位ベクトル $\overrightarrow{e^{x}}$,$\overrightarrow{e^{y}}$,$\overrightarrow{e^{z}}$ をとったものをデカルト座標系と言います。
デカルト座標系では、たとえば、ベクトル $\overrightarrow{OP}$ は
速度や加速度はベクトルですが、方向性が無い時間はベクトルではありません。
ベクトルを図で表示する場合は下図の様に矢印で表し、矢印の元を始点、矢印の先を終点、矢印の長さ部分を有向線分と言います。
ただし、ベクトルでは、始点の位置には関係無く、矢印の向きと長さだけが重要です。 ですから、大きさが等しくて向きが同じ平行なベクトルは同一です。並行で向きが逆なら-符号を付けます。$\vec{a}=-\vec{a}$
(ベクトルはゴシック体で表しますが、間違えやすいので→を付けています)

原点を0とする直交座標系で、x、y、z方向に単位ベクトル $\overrightarrow{e^{x}}$,$\overrightarrow{e^{y}}$,$\overrightarrow{e^{z}}$ をとったものをデカルト座標系と言います。
デカルト座標系では、たとえば、ベクトル $\overrightarrow{OP}$ は
$$\overrightarrow{OP}=a_{x}\overrightarrow{e^{x}}+a_{y}\overrightarrow{e^{y}}+a_{z}\overrightarrow{e^{z}}\tag{1}$$
ただし、$a_{x}$,$a_{y}$,$a_{z}$ は大きさだけを表すスカラー量です ベクトルの一次従属と一次独立の意味
一次従属」や「一次独立」という難しい言葉が出て来るのは、数学に限らず学問の特質ですね。 これらの難しい言葉を理解しなければ理解したことにならないのでしょうが、、、
ベクトルの一次独立というのは、デカルト座標系の任意のベクトルが空間内の3つのベクトルの一次結合で一意的に定まったときに、 この3つのベクトルを一次独立であると言います。
たとえば、下記式2で $\overrightarrow{p}$ が一意的に定まるならベクトル$\overrightarrow{a_{1}}$ ,$\overrightarrow{a_{2}}$ ,$\overrightarrow{a_{3}}$ を、一次独立と言います。
3次元空間で1点を表すには、x、y、z方向の3つの位置情報が必要な訳ですが、そのベクトル版ですね
ベクトルの一次独立というのは、デカルト座標系の任意のベクトルが空間内の3つのベクトルの一次結合で一意的に定まったときに、 この3つのベクトルを一次独立であると言います。
たとえば、下記式2で $\overrightarrow{p}$ が一意的に定まるならベクトル$\overrightarrow{a_{1}}$ ,$\overrightarrow{a_{2}}$ ,$\overrightarrow{a_{3}}$ を、一次独立と言います。
$$\overrightarrow{p}=x_{1}\overrightarrow{a_{1}}+x_{2}\overrightarrow{a_{2}}+x_{3}\overrightarrow{a_{3}}\tag{2}$$
ただし、$x_{1}$ ,$x_{2}$ ,$x_{3}$ は大きさだけを表す実数です。3次元空間で1点を表すには、x、y、z方向の3つの位置情報が必要な訳ですが、そのベクトル版ですね
一次従属は、少なくとも1つは $0$ でない $x_{1} , x_{2} , \cdots\cdots , x_{n}$ の組に対して
$$x_{1}\overrightarrow{a_{1}}+x_{2}\overrightarrow{a_{2}}+\cdots\cdots+x_{n}\overrightarrow{a_{n}}=0\tag{3}$$
となるベクトル $\overrightarrow{a_{1}} , \overrightarrow{a_{2}} , \cdots\cdots , \overrightarrow{a_{n}}$ を一次従属と言います。 行列でベクトルが3つの場合を成分表示すると
たとえば、$a_{1}=e_{y}+e_{z}$ , $a_{2}=3e_{x}+2e_{y}$ , $a_{3}=e_{x}+e_{y}$ では、行列式
$$\begin{pmatrix} a_{1}, &a_{2}, &a_{3} \end{pmatrix} \begin{pmatrix} x_{1} \\x_{2} \\x_{3} \end{pmatrix} =\begin{pmatrix} p_{1}, &p_{2}, &p_{3} \end{pmatrix} \tag{3}$$
式3の右辺が $0$ になるためには$\begin{pmatrix} a_{1}, &a_{2}, &a_{3} \end{pmatrix}$ が $0$ になる必要があります。たとえば、$a_{1}=e_{y}+e_{z}$ , $a_{2}=3e_{x}+2e_{y}$ , $a_{3}=e_{x}+e_{y}$ では、行列式
$$\det(a_{1},a_{2},a_{3})= \begin{vmatrix} 0 & 3 & 1\\ 1 & 2 & 1\\ 1 & 0 & 0 \end{vmatrix}=1\neq 0$$
$0$ にならないので、ベクトル $a_{1}=e_{y}+e_{z}$ , $a_{2}=3e_{x}+2e_{y}$ , $a_{3}=e_{x}+e_{y}$ は、一次独立となります。 因みに、行列式の計算方法は次の様にします。
$$\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{vmatrix} =a_{11}\cdot a_{22}-a_{12}\cdot a_{21}$$ $$\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} =a_{11}\cdot a_{12}\cdot a_{33}+a_{12}\cdot a_{23}\cdot a_{31}+a_{13}\cdot a_{21}\cdot a_{32} -a_{12}\cdot a_{22}\cdot a_{31}-a_{12}\cdot a_{21}\cdot a_{33}-a_{11}\cdot a_{23}\cdot a_{32}$$
列か行の2つが同じなら、この行列式の値は $0$ になります。 一次独立のときには、このベクトルは一意的に定まるので、逆行列が存在します。
式3で表したものは
式3で表したものは
$$\begin{pmatrix} x_{1} \\x_{2} \\x_{3} \end{pmatrix} =\begin{pmatrix} a_{1}, &a_{2}, &a_{3} \end{pmatrix}^{-1} \begin{pmatrix} p_{1} \\ p_{2} \\ p_{3} \end{pmatrix} \tag{4}$$
一次従属と一次独立の関係は、図示すると解りやすいです。
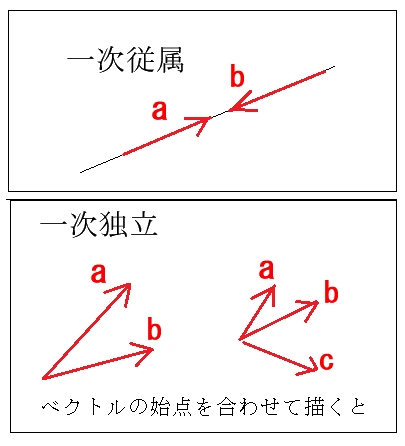
一次従属は、複数のベクトルが直線上にあります。
一次独立は、ベクトルの始点を合わせると、各ベクトルが挟角を作ります。デカルト座標では、一次独立のベクトルは3つです。

一次従属は、複数のベクトルが直線上にあります。
一次独立は、ベクトルの始点を合わせると、各ベクトルが挟角を作ります。デカルト座標では、一次独立のベクトルは3つです。