ベクトルの内積と外積
ベクトルは図示するときには矢印で表され、それが直感と一致しているので理解しやすいですが、 ベクトルの内積や外積となると理解し難くなります。
ベクトル $\mathbf{a}$ と $\mathbf{b}$ の内積と外積を図示すると、次の図の様になります。
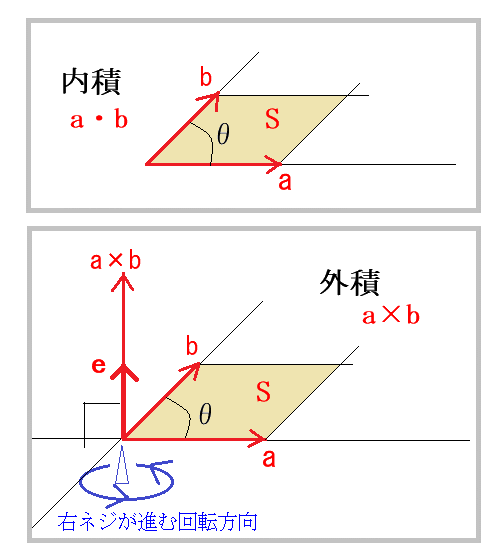
内積は、$\mathbf{a} \cdot \mathbf{b}$ または、$(\mathbf{a},\mathbf{b})$ で表し、次の様に定義されています。
内積は、大きさだけを持つスカラーです(内積はスカラー積とも言います)
ベクトル $\mathbf{a}$ と $\mathbf{b}$ の内積と外積を図示すると、次の図の様になります。

内積は、$\mathbf{a} \cdot \mathbf{b}$ または、$(\mathbf{a},\mathbf{b})$ で表し、次の様に定義されています。
$$\mathbf{a} \cdot \mathbf{b} \equiv \begin{cases} |\mathbf{a}| |\mathbf{b}|\cos\theta & (\mathbf{a}\neq \mathbf{0}\ かつ\ \mathbf{b}\neq \mathbf{0})\\ 0 & (\mathbf{a}= \mathbf{0}\ または \ \mathbf{b}= \mathbf{0}) \end{cases} \tag{1}$$ ただし、$0\leqq \theta \leqq \pi$
$\equiv$ は常に等しいという意味です。$|\mathbf{a}|$ と $|\mathbf{b}|$ は、$\mathbf{a}$ と $\mathbf{b}$ の絶対値です。内積は、大きさだけを持つスカラーです(内積はスカラー積とも言います)
ベクトルの内積はスカラーですが、ベクトルの外積は上図の様に定義される方向をとるので大きさと方向を持つベクトルです。
ベクトルの外積は次の様に定義されています。
単位ベクトル $\mathbf{e}$ が乗じてあるので外積はベクトルになります。
ベクトルの外積は次の様に定義されています。
$$\mathbf{a}\times\mathbf{b}= \begin{cases} |\mathbf{a}| |\mathbf{b}|\sin\theta \ \mathbf{e} & (\mathbf{a}\ ,\ \mathbf{b}\ が一次独立のとき)\\ 0 & ( \mathbf{a} \ ,\ \mathbf{b}\ が一次従属のとき) \end{cases}\tag{2}$$
ただし、$\mathbf{e}$ は、$\mathbf{a}$ と $\mathbf{b}$ を含む面に垂直で右ネジを回して進む方向を正とした単位ベクトルです。単位ベクトル $\mathbf{e}$ が乗じてあるので外積はベクトルになります。
ベクトルの内積の基本計算法則
基本計算法則の証明に必要になるので内積を成分表示で表す式の導く方法を説明します。内積の成分表示
デカルト座標系で、ベクトル $\mathbf{a}$ の成分を $(a_{x}\ a_{y} \ a_{z})$ 、 ベクトル $\mathbf{b}$ の成分を $(b_{x}\ b_{y} \ b_{z})$ とすると
内積$\mathbf{a}\cdot\mathbf{b}=a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}$
内積$\mathbf{a}\cdot\mathbf{b}=a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}$
導き方
ベクトル $\mathbf{a}$ 、$\mathbf{b}$ と、この2つのベクトルが作る角を $\theta$ として、 三角形の余弦定理を適用すると次の図の様になります。
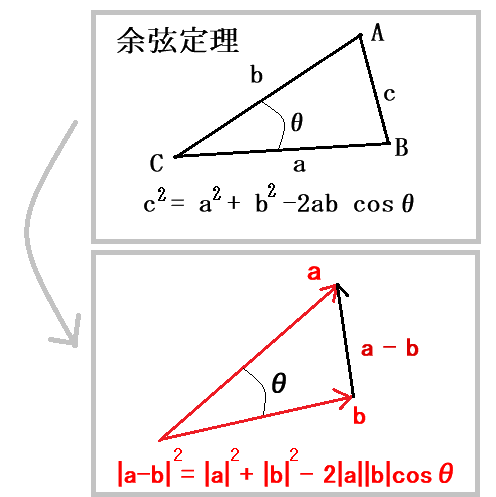
余弦定理を適用して得た式
ベクトル $\mathbf{a}$ 、$\mathbf{b}$ と、この2つのベクトルが作る角を $\theta$ として、 三角形の余弦定理を適用すると次の図の様になります。

余弦定理を適用して得た式
$$|\mathbf{a}-\mathbf{b}|^2=|\mathbf{a}|^2+|\mathbf{b}|^2-2|\mathbf{a}||\mathbf{b}|\cos\theta\tag{3}$$
式3の右辺3項目は内積の定義(式1)より $$|\mathbf{a}||\mathbf{b}|\cos\theta=\mathbf{a}\cdot\mathbf{b}\tag{4}$$
よって式3の内積を左辺に移動させて $$\mathbf{a}\cdot\mathbf{b}=\dfrac{|\mathbf{a}|^2+|\mathbf{b}|^2-|\mathbf{a}-\mathbf{b}|^2}{2}\tag{5}$$
ここで、デカルト座標系で表した$\mathbf{a}$ の成分を $(a_{x}\ a_{y} \ a_{z})$、 $\mathbf{b}$ の成分を $(b_{x}\ b_{y} \ b_{z})$ と置いて式5の右辺を計算すると $|\mathbf{a}|^2=a_{x}^2+a_{y}^2+a_{z}^2$
$|\mathbf{b}|^2=b_{x}^2+b_{y}^2+b_{z}^2$
$|\mathbf{a}-\mathbf{b}|^2=(a_{x}-b_{x})^2+(a_{y}-b_{y})^2+(a_{z}-b_{z})^2$
上の3つの式を式5に代入して整理すると、内積を成分表示した $|\mathbf{b}|^2=b_{x}^2+b_{y}^2+b_{z}^2$
$|\mathbf{a}-\mathbf{b}|^2=(a_{x}-b_{x})^2+(a_{y}-b_{y})^2+(a_{z}-b_{z})^2$
$$\mathbf{a}\cdot\mathbf{b}=a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}\tag{6}$$
になります。 ベクトルの内積の基本計算法則
$\alpha$ を実数として
- $\mathbf{a}\cdot\mathbf{b}=\mathbf{b}\cdot\mathbf{a}$
- $(\alpha\mathbf{a})\cdot\mathbf{b}=\alpha(\mathbf{a}\cdot\mathbf{b})$
証明は次のとおり
左辺 $(\alpha\mathbf{a})\cdot\mathbf{b}$ を成分表示して表してから式6を使って計算すると
$\alpha(a_{x},a_{y},a_{z})\cdot(b_{x},b_{y},b_{z})$ $=(\alpha a_{x},\alpha a_{y},\alpha a_{z})\cdot(b_{x},b_{y},b_{z})$ $=\alpha a_{x} b_{x}+\alpha a_{y} b_{y}+\alpha a_{z} b_{z}$
右辺 $\alpha(\mathbf{a}\cdot\mathbf{b})$ も同様に計算すると
$\alpha(a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z})$ $=\alpha a_{x}b_{x}+\alpha a_{y}b_{y}+\alpha a_{z}b_{z}$
左辺と右辺が等しくなるので正しい。 - $(\mathbf{a}+\mathbf{b})\cdot\mathbf{c}=\mathbf{a}\cdot\mathbf{c}+\mathbf{b}\cdot\mathbf{c}$
証明は次のとおり
左辺 $(\mathbf{a}+\mathbf{b})\cdot\mathbf{c}$ を成分表示して表してから式6を使って計算すると
$((a_{x},a_{y},a_{z})+(b_{x},b_{y},b_{z}))\cdot(c_{x},c_{y},c_{z})$ $=(a_{x}+b_{x},a_{y}+b_{y},a_{z}+b_{z})\cdot(c_{x},c_{y},c_{z})$ $=(a_{x}+b_{x})c_{x}+(a_{y}+b_{y})c_{y}+(a_{z}+b_{z})c_{z}$ $=a_{x}c_{x}+a_{y}c_{y}+a_{z}c_{z}+b_{x}c_{x}+b_{y}c_{y}+b_{z}c_{z}$
右辺 $\mathbf{a}\cdot\mathbf{c}+\mathbf{b}\cdot\mathbf{c}$ も同様に計算すると
$(a_{x}c_{x}+a_{y}c_{y}+a_{z}c_{z})+(b_{x}c_{x}+b_{y}c_{y}+b_{z}c_{z})$
左辺と右辺が等しくなるので正しい。
ベクトルの外積の基本計算法則
$\alpha$ を実数として- $\mathbf{a}\times\mathbf{b}=-\mathbf{b}\times\mathbf{a}$
証明は次のとおり
大きさはどちらも$|\mathbf{a}| |\mathbf{b}|\sin\theta$ ただし、$\mathbf{a}$ から $\mathbf{b}$ への回転方向で右ネジを進ませる方向を正にしているので、 $\mathbf{b}$ から $\mathbf{a}$ への回転方向で右ネジを進ませる方向は逆になるので負になる。 - $(\alpha\mathbf{a})\times\mathbf{b}=\mathbf{a}\times(\alpha\mathbf{b})=\alpha(\mathbf{a}\times\mathbf{b})$
証明は次のとおり
$\mathbf{a}$ と$\mathbf{b}$ が一次従属、または、$\mathbf{a}$ と$\mathbf{b}$ が一次独立でも $\alpha=0$ のときは一次従属となって、
$(\alpha\mathbf{a})\times\mathbf{b}=\mathbf{a}\times(\alpha\mathbf{b})=0$ となる。
$\mathbf{a}\neq0$、$\mathbf{b}\neq0$、$\alpha\gt 0$ のとき、$\theta$ は同じ、右ネジを進める方向を正にとった向きも同じなので
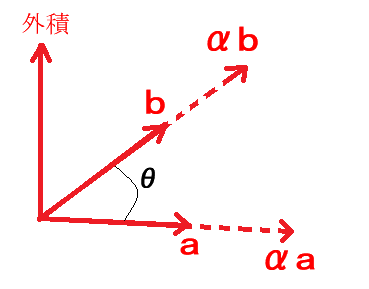
$|\alpha\mathbf{a}||\mathbf{b}|\cos\theta=|\mathbf{a}||\alpha\mathbf{b}|\cos\theta=\alpha|\mathbf{a}||\mathbf{b}|\cos\theta$
$\mathbf{a}\neq0$、$\mathbf{b}\neq0$、$\alpha\lt 0$ のとき、
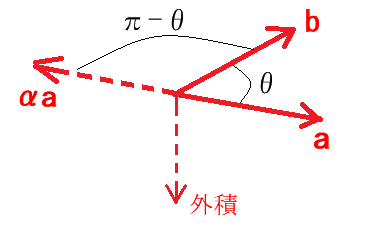
$(\alpha\mathbf{a})\times\mathbf{b}$、$\mathbf{a}\times(\alpha\mathbf{b})$、$\alpha(\mathbf{a}\times\mathbf{b})$の符号が変わるだけで等しい - $\mathbf{a}\times(\mathbf{b}+\mathbf{c})=\mathbf{a}\times\mathbf{b}+\mathbf{a}\times\mathbf{c}$