数の置き換え、置換の種類と積の計算方法
数学での置換は、例えば、
$(1,2,3)$ という3つの整数からなるものを $(1,3,2)$ と順番を変えることを言います。
置換は次の様に2行で表すと判りやすいです。
$\begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}$ ・・・1
上の行は置換する前で、下の行は置換後です。
この様に表すと、$1$ は変わらず、$2$ は $3$ に変わり、$3$ は $2$ に変わったのが容易に判ります。
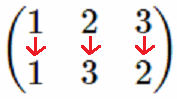
もちろん、この様に表現しても行列とは関係ありません
また、列を変えた $\begin{pmatrix}2&1&3\\3&1&2\end{pmatrix}$ は、 $2$ は $3$ に変わり、$1$ は変わらず、$3$ は $2$ に変わっているので先の1と同じです。
この例では2つの数の順番を変えましたが全ての数の順番を変えることも置換で、数は3つで無くてもかまいません。
$(1,2,3)$ という3つの整数からなるものを $(1,3,2)$ と順番を変えることを言います。
置換は次の様に2行で表すと判りやすいです。
$\begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}$ ・・・1
上の行は置換する前で、下の行は置換後です。
この様に表すと、$1$ は変わらず、$2$ は $3$ に変わり、$3$ は $2$ に変わったのが容易に判ります。
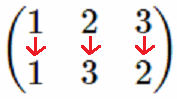
もちろん、この様に表現しても行列とは関係ありません
また、列を変えた $\begin{pmatrix}2&1&3\\3&1&2\end{pmatrix}$ は、 $2$ は $3$ に変わり、$1$ は変わらず、$3$ は $2$ に変わっているので先の1と同じです。
この例では2つの数の順番を変えましたが全ての数の順番を変えることも置換で、数は3つで無くてもかまいません。
たとえば、
また ところで、こんな並び替えをする置換に何の意味があるのだろうと思いますが、簡単な例では複雑な数式を簡便に表したいときに使います。
私が置換を勉強しようと思った切っ掛けは、ベクトルの外積の計算でした。
$$\begin{pmatrix}1&2&3&4&5\\1&2&3&4&5\end{pmatrix}$$
の様に変わっていない置換を「恒等置換」と言いますまた
、 $$\begin{pmatrix}1&4&5&2&3\\2&3&1&5&4\end{pmatrix}$ の行を交換した $$\begin{pmatrix}2&3&1&5&4\\1&4&5&2&3\end{pmatrix}$$ を「逆置換」と言います。
置換を $\sigma$ で表すなら逆置換は $\sigma^{-1}$ と表します。私が置換を勉強しようと思った切っ掛けは、ベクトルの外積の計算でした。
互換
最初の挙げた置換の例 $\begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}$ の下図の水色で囲った2列の部分の置換を「互換」と言います。
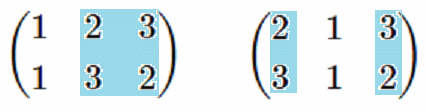
そして、 $(2,3)$ または $(3.2)$ と簡単な表記にすることが出来ます。
$2$ が $3$ に置き換わり、$3$ は $2$ に置き換わっています。表記されて居ない数 $1$ はそのまま変わって居ないことを意味します。
置換する数が多くなれば互換が複数存在することがあります。
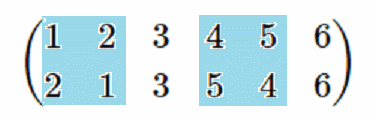
$(1,2)(4,5)$ は後で説明する互換の積で、$4$ は $5$ に置き換わり、$5$ は $4$ に置き換わり、$1$ は $2$ に置き換わり、$2$ は $1$ に置き換わり、$3$ と $6$ はそのままを表しています。
互換は重要なのでよく理解する必要があります。
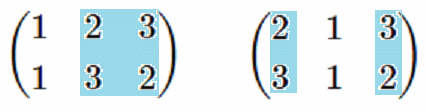
そして、 $(2,3)$ または $(3.2)$ と簡単な表記にすることが出来ます。
$2$ が $3$ に置き換わり、$3$ は $2$ に置き換わっています。表記されて居ない数 $1$ はそのまま変わって居ないことを意味します。
置換する数が多くなれば互換が複数存在することがあります。

$(1,2)(4,5)$ は後で説明する互換の積で、$4$ は $5$ に置き換わり、$5$ は $4$ に置き換わり、$1$ は $2$ に置き換わり、$2$ は $1$ に置き換わり、$3$ と $6$ はそのままを表しています。
互換は重要なのでよく理解する必要があります。
巡回置換
$$\begin{pmatrix}1&2&3&4&5&6\\2&4&3&1&5&6\end{pmatrix}$$
の置換は、元に戻る置換を1つ含んでいます。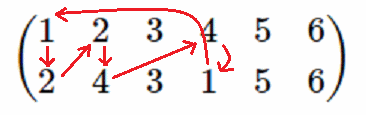
赤い矢印で示した様に $1\to2\to4\to1$ と辿ると回るので巡回置換と言います。
巡回置換は、$1$ から始めても $2$ から始めても $4$ から始めても同じなので
巡回置換の簡便な表記 $(1,2,4)$ と $(2,4,1)$ と $(4,1,2)$ は同じ意味です。ここに表示されて居ない数 $3,5,6$ は変わらないという意味です。
先に説明した「互換」も2列の間で巡回しているので、互換は巡回置換の特別の場合です。
巡回置換は複数の互換の積で表されます。
たとえば、巡回置換 $(1,2,4)$ は、互換 $(1,4)$ と互換 $(1,2)$ の積 $(1,4)(1,2)$ で表されます。
置換の積の計算方法は、次の項で説明しますが、
巡回置換は複数の互換の積で表されます。
たとえば、巡回置換 $(1,2,4)$ は、互換 $(1,4)$ と互換 $(1,2)$ の積 $(1,4)(1,2)$ で表されます。
置換の積の計算方法は、次の項で説明しますが、
$n$ 個からなる巡回置換 $$(a_{1},a_{2},a_{3},\ldots\ldots,a_{n-2},a_{n-1},a_{n})$$ は
$n-1$ 個の互換置換の積 $$(a_{1},a_{n})(a_{1},a_{n-1})(a_{1},a_{n-2}),\ldots\ldots,(a_{1},a_{3})(a_{1},a_{2})$$ で表されます。
一番最初の数と最後から数を1つずつ取って組み合わせるだけです。 $n-1$ 個の互換置換の積 $$(a_{1},a_{n})(a_{1},a_{n-1})(a_{1},a_{n-2}),\ldots\ldots,(a_{1},a_{3})(a_{1},a_{2})$$ で表されます。
置換は幾つかの巡回置換で表され、巡回置換は幾つかの互換で表されます。
ですから、置換は幾つかの互換で表すことが出来ます。
ただし、同じ置換でも互換の積は幾通りもあることがあります。
(ただ、互換の個数が偶数か奇数か置換によって決まります。これは後で説明する置換の符号の決定に使います)
ですから、置換は幾つかの互換で表すことが出来ます。
ただし、同じ置換でも互換の積は幾通りもあることがあります。
(ただ、互換の個数が偶数か奇数か置換によって決まります。これは後で説明する置換の符号の決定に使います)
置換の積の計算
「積」と言うと掛け算だと思いますが、置換の積は計算を必要としません(表記が行列と同じですが行列ではありません)
しかし、交換法則が成り立たないので計算の順番に注意が必要です。
交換法則というのは、乗算なら $a\times b=b\times a$ が成り立つ場合を乗算は交換法則が成り立つと言います。
置換 $\sigma$ と置換 $\tau$ では、$\sigma \tau \neq \tau \sigma$ です。
また、$\sigma \tau$ の積の計算では、2つ目の $\tau$ から先に計算します。
たとえば
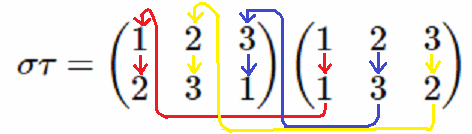
しかし、交換法則が成り立たないので計算の順番に注意が必要です。
交換法則というのは、乗算なら $a\times b=b\times a$ が成り立つ場合を乗算は交換法則が成り立つと言います。
置換 $\sigma$ と置換 $\tau$ では、$\sigma \tau \neq \tau \sigma$ です。
また、$\sigma \tau$ の積の計算では、2つ目の $\tau$ から先に計算します。
たとえば
$$\sigma =\begin{pmatrix}1&2&3\\2&3&1\end{pmatrix}$$ と $$\tau =\begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}$$ の積$\sigma\tau$ は
$$\sigma\tau =\begin{pmatrix}1&2&3\\2&3&1\end{pmatrix} \begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}$$
次の図の矢印の様に前の()内には同じ数を辿って答えを得ます。$$\sigma\tau =\begin{pmatrix}1&2&3\\2&3&1\end{pmatrix} \begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}$$
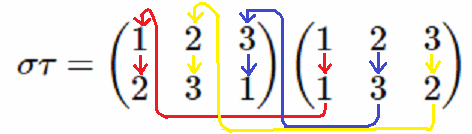
$$\sigma\tau =\begin{pmatrix}1&2&3\\2&1&3\end{pmatrix}$$
置換の符号を求める方法
先に「互換の個数が偶数か奇数か置換によって決まります。」と説明しました。
互換の数が偶数のときは $1$
互換の数が奇数のときは $-1$
と置換に正負の符号を付ける定義をします。
br>
巡回置換では4個の数を使って居るので互換で表せば3個、それに互換が1個なので合計4個、偶数なので符号は $1$
互換の数が偶数のときは $1$
互換の数が奇数のときは $-1$
と置換に正負の符号を付ける定義をします。
br>
$$\begin{pmatrix}1&2&3\\1&2&3\end{pmatrix}$$
は置換しても変わらないので恒等置換で、互換数は $0$ で偶数、符号は $1$ $$\begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}$$
は、$2\to3$、$3\to2$ で 互換は $(2,3)$ 互換数は $1$ で奇数、符号は $-1$ $$\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}$$
は、$1\to3$、$3\to2$、$2\to1$ で巡回置換 $(1,3,2)$ 数字は3個使って居るから $3-1$ 個の互換の積で表されるので互換数は偶数、符号は $1$ $$\begin{pmatrix}1&2&3&4&5&6&7\\4&1&2&3&5&7&6\end{pmatrix}$$
は、$1\to4$、$4\to3$、$3\to2$、$2\to1$ で巡回置換 $(1,4,3,2)$ と $6\to7$、$7\to6$ の互換 $(6,7)$ の積で表されます。巡回置換では4個の数を使って居るので互換で表せば3個、それに互換が1個なので合計4個、偶数なので符号は $1$
置換の符号のベクトルへの応用の初歩
デカルト座標系に於いて、基本ベクトル $\mathbf{e_{x}}$ $\mathbf{e_{y}}$ $\mathbf{e_{z}}$ は互いに直交しているので外積の定義から
$\mathbf{e_{x}}=\mathbf{e_{y}}\times \mathbf{e_{z}}$
$\mathbf{e_{y}}=\mathbf{e_{z}}\times \mathbf{e_{x}}$
$\mathbf{e_{z}}=\mathbf{e_{x}}\times \mathbf{e_{y}}$
$\mathbf{e_{x}}=-\mathbf{e_{z}}\times \mathbf{e_{y}}$
$\mathbf{e_{y}}=-\mathbf{e_{x}}\times \mathbf{e_{z}}$
$\mathbf{e_{z}}=-\mathbf{e_{y}}\times \mathbf{e_{x}}$
が、上記6つの式を$\mathbf{e_{y}}=\mathbf{e_{z}}\times \mathbf{e_{x}}$
$\mathbf{e_{z}}=\mathbf{e_{x}}\times \mathbf{e_{y}}$
$\mathbf{e_{x}}=-\mathbf{e_{z}}\times \mathbf{e_{y}}$
$\mathbf{e_{y}}=-\mathbf{e_{x}}\times \mathbf{e_{z}}$
$\mathbf{e_{z}}=-\mathbf{e_{y}}\times \mathbf{e_{x}}$
$\mathbf{e_{x}}=\mathbf{e_{1}}$ $\mathbf{e_{y}}=\mathbf{e_{2}}$ $\mathbf{e_{z}}=\mathbf{e_{3}}$ として、置換の符号を利用して書くと
$\mathbf{e_{i}}\times\mathbf{e_{j}}= \begin{cases}\mathbf{e_{k}} & \mathbf{互換数が偶数} \\ -\mathbf{e_{k}} & \mathbf{互換数が奇数} \end{cases}$
と簡単になります。 $\mathbf{e_{z}}$ と $\mathbf{e_{x}}$ の外積の置換は $\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}$ 数3個の巡回置換なので $3-1$ で偶数、符号は $1$ で、$\mathbf{e_{z}}\times\mathbf{e_{x}}=\mathbf{e_{y}}$
$\mathbf{e_{y}}$ と $\mathbf{e_{x}}$ の外積の置換は $\begin{pmatrix}1&2&3\\2&1&3\end{pmatrix}$ 互換が1個なので奇数、符号は $-1$ で、$\mathbf{e_{y}}\times\mathbf{e_{x}}=-\mathbf{e_{z}}$
$\mathbf{e_{i}}\times\mathbf{e_{j}}= \begin{cases}\mathbf{e_{k}} & \mathbf{互換数が偶数} \\ -\mathbf{e_{k}} & \mathbf{互換数が奇数} \end{cases}$
と簡単になります。 $\mathbf{e_{z}}$ と $\mathbf{e_{x}}$ の外積の置換は $\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}$ 数3個の巡回置換なので $3-1$ で偶数、符号は $1$ で、$\mathbf{e_{z}}\times\mathbf{e_{x}}=\mathbf{e_{y}}$
$\mathbf{e_{y}}$ と $\mathbf{e_{x}}$ の外積の置換は $\begin{pmatrix}1&2&3\\2&1&3\end{pmatrix}$ 互換が1個なので奇数、符号は $-1$ で、$\mathbf{e_{y}}\times\mathbf{e_{x}}=-\mathbf{e_{z}}$