地球の何処が引力が強いか
地球上にあるものは、ほぼ地球の中心に向かって引かれています。私たちはこの力を重さとして感じています。
では、地球に引かれる力が一番弱いところは地球の何処か?という、一見戸惑いますが、言われてみれば当たり前という話です。 厳密に計算するには地球を細かく分けてそのそれぞれの関係で計算して合力を求めるのですが、ここでは極々大雑把に考えています。
ニュートンの万有引力の法則
物体間に作用する引力は、ニュートン(Isaac Newton 1642~1727)によって、距離R、質量m1 質量m2二つの物体間に働く引力Fは、万有引力定数をKとすると
F=K×m1×m2÷(R*R)
で表されています。
引力は物体の質量に比例し、物体間の距離の二乗に反比例しています。
勿論、実際の場面では引力は無数の物体間に働く引力のベクトル和となります。
力の合成
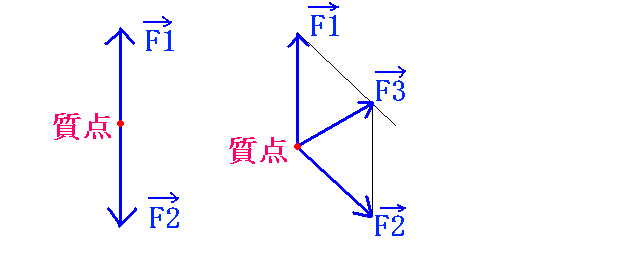
力のベクトルというのは、力の大きさと方向を持ったものです。
下図の左の場合は、力F1と力F2が180度の向きに質点に作用しているので、力F1と 力F2の大きさが等しければ質点はどちらにも引っ張られません。
しかし、力F1と力F2の大きさが異なれば、大きい方に力F 1と力F2の大きさの差だけ大きい力の方向に引っ張られます。
右図のように力F1と力F2の向きが180度で無い場合は、力F1と力F2で平行四辺形を作った対角線F3の方向に引っ張られます。
例えば、貴方は地球と引力を及ぼし合っていますし、同時に目の前のパソコンとも、隣にある本とも、その他、諸々の物体、遠くは恒星とも引力を及ぼし合っています。
この場合は物体を質量はあるが体積が無い質点と考えていますが、物体は体積があり、近くの物体同士でしたら質点と考えたら正確な答えは出ません。
頭とパソコンの位置関係、足とパソコンの位置関係は大きく異なります。
仮想の質点と地球との引力を考察する
前知識を得たところで、真球体で全てのところで質量が同じの地球表面上に質点を置いたと仮定し、この質点と地球との間に働く引力を考えてみましょう。
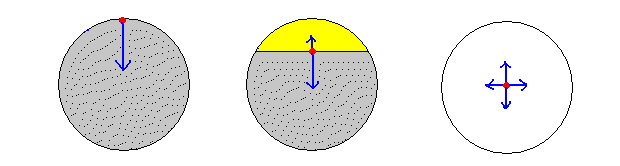
上図左は質点(赤点)を地球表面に置いた、中央は地球内部に質点を入れた、右図は質点を地球の中心に入れた、それぞれのイメージ図です。
質点を表面に置いたときには、質点と地球上の全ての部分(灰色部分)の間に働く引力は下向きに作用します。
質点を内部に入れた場合には質点と質点より上の部分(図の黄色部分)に働く引力は上向きに作用するので、下向きに作用する引力が減らされることになります。
質点を地球の中心に置くと、質点は全ての方向から同じ大きさの引力を受けるので引力が0になってしまいます。
引力の大きさは、 表面>内部>中心部 となります。
実際の地球は真球体では無く、質量は場所によって不均一です(マグマや鉱脈、地下水などがあるため)
形や不均一を除いても、中心部に行くほど質量が大きくなっているので(密度が大きい)、 質点を地球内部に入れて行くと、質量の大きい部分に近づくために引力は表面より増して行きますが (万有引力の法則によれば、距離が半分になると、引力は4倍になります)、地球の中心部に入れば全ての方向から引っ張られるので引力は一番小さいということになります。