コマが倒れない理由の簡単な説明

ニュートン（1642-1727）の「運動の三法則」の一つに 慣性の法則 があります。 これは、「 静止または一様な直線運動をする物体は、力が作用しない限り、その状態を持続する」というものです。
たとえば、投げたボールは外部から力を加えない限りその方向に飛び続けます。 地球上で投げると、外部からの力（空気の抵抗と地球の引力）によって落下しますが、宇宙空間で投げれば、何処かの星の引力圏に入るまで飛び続けるでしょう。

下図の「こま（独楽）」は時計方向に回っていると仮定し、この独楽の一部（図の青い部分）に注目します。

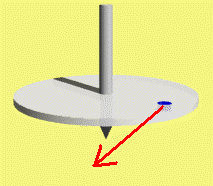
青い部分は、独楽の軸を中心とした、この部分を含む円の接線方向（赤の矢印）に向かって運動しています。 接線と言うのは、円上の点と、この点と円の中心を結んだ直線と直角をなす直線です。
慣性の法則によって、青い部分は外から力が加わらない限り、赤い矢印の方向に運動し続けようとします。 独楽の全ての部分が、青い部分と同じように今の状態を保とうとするので、独楽に軽く指を触れたぐらいでは倒れないのです。
この性質を理由したのが主に船舶に使われていた ジャイロコンパスや　玩具の地球コマ です。
同じ状態を保とうとする能力は質量が大きいほど大きく、加える力が大きいほど大きいので、ジャイロコンパスは、独楽の外側を重くした、大きな独楽を高速で回転させるものでした。

物を飛ばすとき、回転させると、独楽と同じように安定して飛びます。 このため、無人ロケットなどは回転させることがありますし、曲芸で物を投げるときもその物を回転させます。
また、円盤が大きく、かち、質量が大きければ、外部からの力に余り影響を受けないで回るので、 自動車のエンジンのように力を出さない時間がある物に大きな独楽（はずみ車）を回させて力を均一にさせるために利用されます。
（シリンダー内で燃料を爆発的に燃やして力を得るエンジンでは、燃料が燃えたときにしか力が出ない。蒸気機関や電動モーターでも同じ力がいつも出ている訳では無い）