容器から一定の速度で水が出るマリオットの器
器の孔から水が流れ出る速度
浴槽や洗濯機から水を抜くとき、始めは早く水位が下がるのですが、徐々に水位の下がり方が遅くなるのに苛立った経験がおありでしょうか。
始めは水の量が多いために下図のhが大きいので重力による位置エネルギーが大きいために水が出る速度が大きく、水が出続けるとhが小さくなるので位置エネルギーが小さくなって水の出る速度が遅くなります。
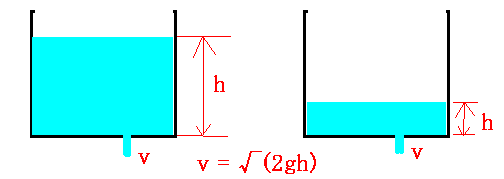
容器に開けた孔が小さいときはガリレオの弟子のトリチェリは、水が出る速度$V$は
$g$は重力加速度です。
容器の孔が小さいときという条件は、トリチェリの式が孔に集まる容器の中の水の速度を0として導いているからです。
容器の孔から水が出て孔から水面までの高さ$h$が減って行くにつれて水の出が遅くなって、時間の割には水が抜けなくてイライラして来るのが平方根で表されています。
水が出る孔$s$が小さいという条件で、水面の面積を$S$として、水面の高さが$h_{0}$から$h_{1}$に変わるまでの時間$t$は
始めは水の量が多いために下図のhが大きいので重力による位置エネルギーが大きいために水が出る速度が大きく、水が出続けるとhが小さくなるので位置エネルギーが小さくなって水の出る速度が遅くなります。

容器に開けた孔が小さいときはガリレオの弟子のトリチェリは、水が出る速度$V$は
$$ V = \sqrt{2gh}$$
で求められることを導きました。 $g$は重力加速度です。
容器の孔が小さいときという条件は、トリチェリの式が孔に集まる容器の中の水の速度を0として導いているからです。
容器の孔から水が出て孔から水面までの高さ$h$が減って行くにつれて水の出が遅くなって、時間の割には水が抜けなくてイライラして来るのが平方根で表されています。
水が出る孔$s$が小さいという条件で、水面の面積を$S$として、水面の高さが$h_{0}$から$h_{1}$に変わるまでの時間$t$は
$$ t = \sqrt \frac{2}{g} \cdot \frac{S}{s} \cdot \sqrt{h_{0} -h_{1}}$$
水が出る速度を一定にしたものに、マリオットの器 があります。マリオット(1620-1684?)はフランスの物理学者です。
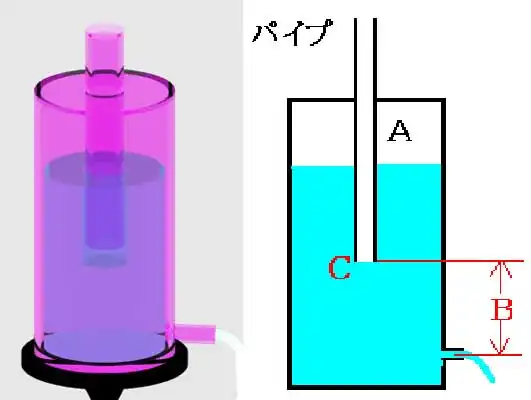
水が流れ出ると、容器内の圧力が下がってパイプから外の空気が入り、水の中をブクブクと通ってAに入り、水の重量とつり合う位置で止まります。
パイプは外部と繋がっているので、その先端Cの位置での位置エネルギーはBの高さになります。
このため、出口から出る水の速度はBの高さに依存し、パイプの先端Cの位置より水位が下がらない限りBの高さは変わらないので、ここまでは一定の速度で流れ出ます。