ガリレイの相対性原理とガリレイ変換とは

相対性原理というとアインシュタインを思い浮かべますが、言葉だけをとれば、ガリレオ・ガリレイ【Galileo Galilei】が提唱した相対性原理が先になります。
ガリレイの相対性原理は日常生活の中で経験することなので解かりやすいものです。たとえば、電車の中で手に持った物をどちらの方向にも力を加えずに落としてみてください（自由落下させる）。 電車が止まっていても等速で動いていても電車内に居る人から見れば落とした物は真下に落ちます。
物を落とすときの手の位置を座標Ｘ－Ｙの原点にとれば、電車が止まっているときと動いているときでは座標の原点の位置は違いますが、どちらも原点を通るＹ軸上を通って落ちているので同じ自由落下の法則で説明できます。 電車といわず、地球上で物を落としても 地球が動いているにも関わらず地球上に居る人から見たときには物は真下に落ちます。
今度は等速で動いている電車の外で見ている人を座標Ｘ－Ｙの原点に持ってきてみます。
Ｘ軸の＋方向に等速Ｖで動いている電車内で物を落とすと、物は放物線を描きなら落下します。

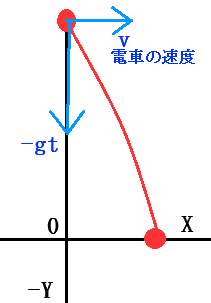
このとき、物に働いている力は、真下に落とそうとする力(地球とその物の間に働く万有引力)と、等速で動いている電車と一体として動いていた物が持つＸ軸＋方向の力です。 真下方向へは自由落下の法則に従っています。
要するに、座標の原点を静止させても等速で動かしても同じ力学の法則が摘要できるというのがガリレイの相対性原理です。

ガリレイ変換

座標が止まっているか、等速で動いているかだけの違いですから、それぞれの座標上で表される物体の運動は相互に変換できます。
たとえば、止まっている電車内で物を自由落下させた運動を、速度Ｖで走っている電車内で自由落下させた物に摘要するには、落下させる物にＸ軸方向の初速Ｖを加えるだけです。 これをガリレイ変換と呼びます。