マイケルソンとモーレーの実験

ニュートン（Isaac Newton 1642-1727）は、全ての物体の運動が計算によって判明すると言わせるまでに力学を発展させました。 たとえば、ケプラーが観測結果から惑星の運動を求めたのに対し、ニュートンは万有引力を導入することによって計算で求めました。（正確な値を求めるには、求める時点での太陽や月、各惑星の位置を考慮しなければならないので現在でも難しいものです）
しかし、１８８７年、地球の運行速度を測る実験によってニュートン力学は破綻します。 ニュートン力学では、宇宙を含むこの世界には絶対的な時間が流れ、空間も絶対的なものと考えています。 これは、宇宙の何処に居ても地球と同じ時間が流れ、位置関係も変わらないというもので、私たちの日常生活の範囲内では現在でもごく当たり前の考えです。北海道にある時計が示す１秒間と東京や沖縄にある時計の１秒間は同じですし、地震で地殻が移動しない限り、距離と方角も変わりません。

マイケルソン （A.A.Michelson 1852-1931）は、有線電話を発明したベル（Alexander Graham Bell)の支援を受け、モーリー(E.W.Morley 1838-1923)と共に宇宙船地球号の絶対速度を測ろうとしました。
当時、光はニュートン力学に従ってエーテルという媒質を伝わる波と考えられ、地球はエーテルの中を動いていると考えられていました。 そこで、彼らは下図の方法で地球の速度を測ろうとしました。

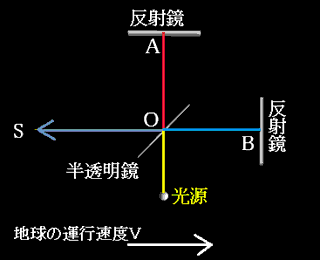
一つの光源（ナトリウムランプ）から出た光を、ハーフミラー（半透明鏡）で地球の公転方向とそれに直角方向に分け、そこから同じ距離にある反射鏡に当て、反射して返ってきた光を再び合わせ、光の干渉縞を観察するというものでした。
上図において、A-O間とB-O間は同じ距離です。 この距離をL、光の速度を$C$、地球の公転速度を$V$とすると、半透明鏡上のO点で分かれた光が公転方向にある反射鏡Bに当たり、反射してO点に戻るまでの時間$T_{1}$は

$$T_{1} = \frac{2CL}{C^{2} - V^{2}} $$

となります。

他方、O点で分かれた光が公転方向と直角方向に進み、A点で反射してO点に戻るまでの時間$T_{2}$を求めるには、先ず、速度$V$で流れているエーテルの中を流れと９０度方向に進む光の速度を求めることから始まります。
下図の関係があるので、

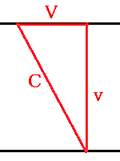
エーテルの流れと直角方向の光の速度$v$は

$$ v = \sqrt {C^{2} - V^{2}} $$

この速度で距離$L$を往復するので、求める時間$T_{2}$は

$$ T_{2} = \frac{2L}{\sqrt{C^{2} -V^{2}}} $$

となります。

上記の計算で解かるように、エーテルを媒質と考えたときの光の速度は公転方向と直角方向では異なるので、 二つの光が合わさったときには光の位相がずれ、干渉縞が観察されるはずでした。 （干渉の身近な例はシャボン玉が虹色に見えることです。シャボン玉の厚みのある膜の表面と裏側で反射した光が干渉して出来ます。 太陽光は色々な波長の光で出来ているので、シャボン玉での光の干渉は色として観察されます。
この実験で使われた光は、単色を発するナトリウム灯なので干渉は縞として観察されます）

しかし、実験結果は予測に反して、公転方向とそれと直角方向の経路を通った光の速度に変化はありませんでした。
$T_{1} = T_{2}$になるためには、地球の運行速度$V$が$0$になる必要がありますが、地球が動いているのは確かなので、 エーテルが無いと考えれば、光の速度は地球の運行速度の影響を受けないと考えられます。 すなわち、光の速度に関しては、速度は常に一定で合成は出来ないということです。
光（電磁波）の速度は、マクスウェルの電磁理論によって導かれ、それによれば、光の速度は光を出しているもの（波源）の運動状態には無関係です。