2つのカメラで距離を測る方法
自動車の自動ブレーキのポイントは改めて言うまでもなく1秒でも早く障害物を発見することです。 街乗りでも制限時速50kmの所は多いので、時速50kmでブレーキを掛けて停まるまでの制動距離を20mとすれば、少なくとも20m先にある物が停止しているのか動いているのか確認する必要があります。 ここでは、2つのカメラを使った方法で対象物までの距離を測る方法を考えてみましょう。
基本的には長さが判明している辺の両端からの対象物が見える角度から距離を求める三角測量と同じですが、 対象物にカメラを向けて角度を測っている時間は無いと思うので、二つのカメラの光軸が平行に正面を向いていると仮定しましょう。
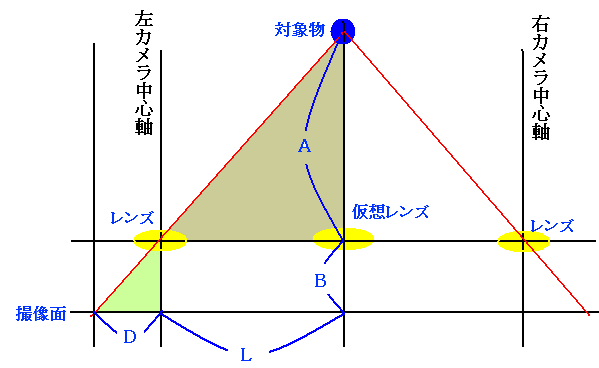
図の中央の仮想レンズで、薄いレンズの公式から f をレンズの焦点距離とすると
$$\frac{1}{A} + \frac{1}{B} = \frac{1}{f} \tag{式1}$$
図中の色を塗った二つの三角形は相似なので $$A:L = B:D \tag{式2}$$ 式1から $$ B = \frac{AD}{L} \tag{式3}$$ 式2から $$ B = A\frac{f}{A-f} \tag{式4}$$
式3と式4からカメラレンズから対象物までの距離Aは $$A = f(1+ \frac{L}{D}) \tag{式5}$$ $$ d = L \frac{f}{A-f} \tag{式6}$$
右カメラも同様になりますが、撮像面に出来る像は左カメラとは逆方向にずれます。 ですから、左右のカメラで結像されたものを重ね合わせれば、その横方向のずれている距離、 左右のカメラの間隔、カメラレンズの焦点距離から対象物までの距離が求められます。
式6から、左右のカメラの間隔$2L$が大きい方が像のずれ$D$が大きくなって距離の判別が付きやすくなるのが判ります。
もちろん、レンズの収差によって図に示したように正確な位置には結像しないでしょうし、 カメラとその対象物までの距離が近くなれば図の三角形の相似関係が崩れてしまうので上記の様な簡単な計算では求められなくなりますが