人が移動できる時空の範囲

“タイムトラベラー 時空の旅人”
小説には未来から来た少年の話がありますね。 “タイムマシン”“タイムトラベ ラー”という響きは、「創り話」と思いながらも映像化されたものに胸をときめかした少年時代を思い起こさせます。
タイムトラベラーは“時空”を旅すると言いますから、先ず、時空の距離をどのように表すか考えてみましょう。
時空の“空”は３次元空間を意味します。
私たちが普通に考える“Ｘ－Ｙ－Ｚ座標”で示される空間です。
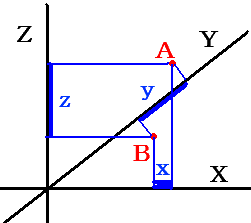
ですから、或る点Ａから点Ｂまでの距離ｓの二乗は
ｓｓ＝ｘｘ＋ｙｙ＋ｚｚ
で表されます。
但し、ｘはＸ軸上に投影したＢからＡまでの距離、 同様にｙはＹ軸上、ｚはＺ軸上での距離を表します。

問題は時空の“時”を“空”に結合する方法です。
ミンコフスキーは、時空での距離Ｓとすると
ＳＳ＝ｘｘ＋ｙｙ＋ｚｚ－(ｃｔ)(ｃｔ)
或いは
Ｘ、Ｙ，Ｚ軸の“光の秒速”で目盛り、時間軸の１秒と対応させて
ＳＳ＝ｘｘ＋ｙｙ＋ｚｚ－ｔｔ
と表しました。
但し、ｃは光速、ｔは時間です。
３次元空間での変位をｓｓとまとめてしまえば
ＳＳ＝ｓｓ－ｔｔ　　　・・・式８
－ｔｔの平方根をとると虚数になりますが、これ自体は数学的意味しかありません。
時間軸は虚数だと言われても意味不明です。虚数だから時間が見えないという方も居ますが。

さて、式８で空間と時間の変位が結合できることが判りました。
例えば、あなたが居る位置から光が発射されたとします。この光が走る軌跡は、時間１秒当たり空間の変位３０万ｋｍを１としていますから、 ４５度の傾きを持った直線で表され、３６０度ひと回りさせるとあなたを頂点とした逆円錐と貴方の下には貴方を頂点とした円錐ができます。 この光の軌跡が作る線を“光の世界線”、円錐を“光円錐”と呼びます。

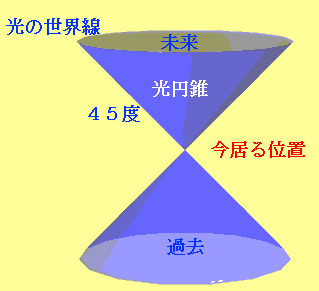
“世界線”というのは、時空の中で物が動く線です。（ミンコフスキーが初めて使った用語です）
貴方も私も時空の中では各々の世界線の上に居ます。

“光円錐”は、私たちが採り得る世界線が含まれる範囲です。光より速く移動できないのですから、私たちの世界線が４５度より小さいのは明らかです。
下に出来る円錐は、あなたや私が今の瞬間まで通ってきた世界線が含まれる範囲を表します。

ここで、貴方がタイムマシンに乗って１０年前の自分に会うことを考えてみましょう。
自分に会うということは、１０年前の世界点（世界線上の時間によって特定される点）に世界線を向けなければなりません。 しかし、秒速１００ｋｍの乗り物に乗っても１分ちょっとしか世界線は変化しません。世界線の傾きa とすると　tan(a)=100/300000
アインシュタインの“特殊相対性理論”は光より早く信号を伝えるものは存在しないと言っているので、世界線を傾けて過去に戻る方法を否定しています。
では、過去に戻れないか、というと、同じくアインシュタインの“一般相対性理論”は、時空は曲げられると言っているので、時空を曲げて過去に戻る方法があるかも知れません。