潮汐力・潮の満ち引きが起きる理由と大潮小潮とは何か？

海面の高さを表す潮位は１日２回高くなって１日２回低くなります。海面の高さが最高になったときを満潮、海面の高さが最低になったときを干潮と言います。
潮の満ち引きが月の引力によって起こることは知られていますが、どのような仕組みで海面の高さが変わるのでしょうか？

海水が月に引っ張られるだけなら満潮は、月が見える時間の日に１回のはずですが、約半日後にもあります。
ということは、地球を挟んで月が反対側にあるときも満潮になり、海面は月とは反対側に引っ張られていることになります。
引力によって海水が引っ張られるというイメージではありません。

潮汐力・潮の満ち引きは空間の歪みによって生じる

月によって地球の各部には下図で示した青矢印の様に万有引力が働いています。

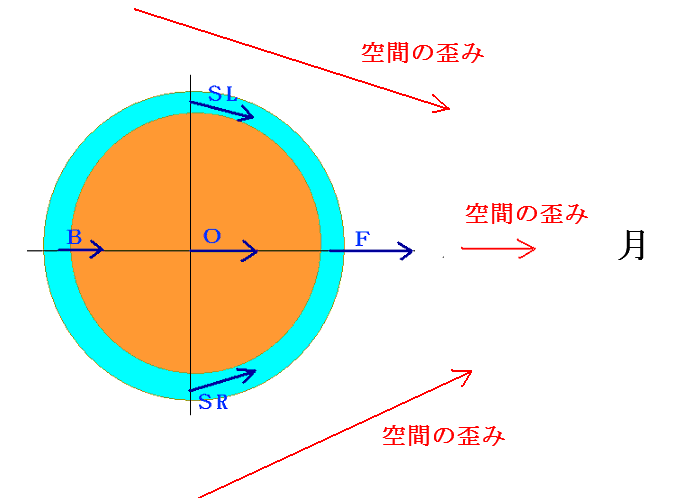
月は右横方向にあるとし、青矢印の方向は力の向き、矢印の長さは力の大きさを示しています。
引力の大きさは距離の二乗に逆比例するので、月に近い点に働いているＦが最も大きく、次は地球の中心に働いているＯ、一番弱い引力はＦより地球の直径だけ離れているＢです。
上図で示した力、Ｏ，Ｆ，ＳＲ、Ｂ、ＳＬは万有引力によるものですが、万有引力は質量によって空間が歪んだことによって生じます。空間の歪みは歪みの原因になっている月によって起きているので、空間の歪みは月から離れているＢは月に近いＦより小さく、月の中心と地球の中心を結んだ線からずれている地球の横では空間は月に向かって歪んでいるので横に働く力、ＳＲとＳＬが斜めになっているのも理解出来ると思います。

地球の中心に働いている引力Ｏを基準にして、引力Ｆと引力Ｂの差を取ると、下図の様になります。

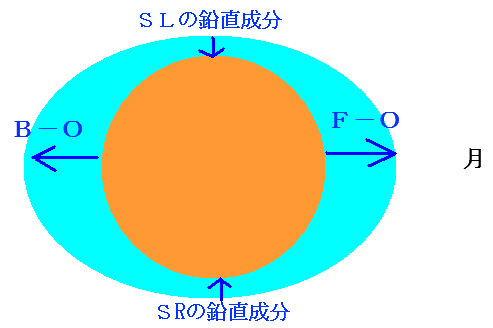
引力Ｆ，引力Ｏ，引力Ｂの大きさは、Ｆ＞Ｏ＞Ｂなので、月に面した側に働いている力（Ｆ－Ｏ）は０より大きく、月の反対側の働く力（Ｂ－Ｏ）は０より小さくなります。
月に面した方向を正にして計算しているので、月の反対側に働いている力（Ｆ－Ｏ）の向きは反対方向になります。このため、月に面していない側でも海水が外側に引っ張られて潮位が高くなります。

潮の満ち引きが起きる理由を直感的に説明すると

下図の様に傾斜した滑らかな（摩擦が無い）台の上を、赤色の球、青色の球、黄色の球が転がり落ちていると想像してください。
この滑らかに傾斜した台は、横方向が質量を持つ物体までの距離（右へ行くほど物体までが近くなる）、縦方向が万有引力の大きさを表すように作ってあります（下に行くほど万有引力が大きくなる）
想像ついでに、青色の球には貴方が乗っていて、赤色の球と黄色い球が見えるとします。

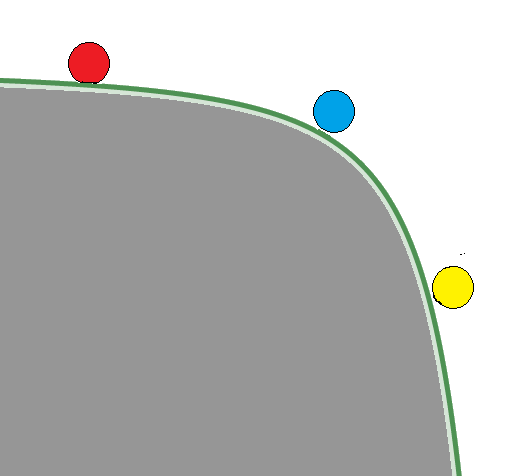
この３つの球が転がり始めるときに力を加えなければ、球が滑り落ちる速さは、
赤色の球の速度＜青色の球の速度＜黄色の球の速度
となるのは直ぐに理解出来ますね。
ここで、青色の球に乗っている人が赤色の球を見ると、赤色の球の速度が遅いので赤色の球が遠ざかっているように見えます。
黄色の球を見ると黄色の球の速度が速いので黄色の球も遠ざかって見えます。
赤色の球と黄色の球を海面、青色の球を地球の中心、３つの球が滑り落ちる傾斜を質量によって生じる空間の歪みとすると、片側に引っ張られて居るだけなのに地球の中心から見れば両側の海面が膨らんでいることになります。

大潮小潮が起きる理由

満月や新月のときは、太陽と地球、月がほぼ一直線上に並ぶので、太陽の引力も重なって、干満の差が大きくなる「大潮」になります。
太陽と月の位置関係が地球から見てほぼ９０度になる上弦と下弦では、太陽による引力と月による引力が打ち消し合って干満の差が小さい「小潮」になります。
万有引力は質量に比例するので、月より質量がはるかに大きい太陽の引力を最も受けているのですが、上図の（Ｂ－Ｏ）と（Ｆ－Ｏ）の潮汐力は、地球の中心と地球の表面上との引力の差なので、月よりはるかに遠い所にある太陽までの距離に対して地球の半径が小さすぎるので、地球から月までの距離に対して近い月による潮汐力が太陽による潮汐力より２倍大きくなっています。