アルキメデスの原理と船が傾く理由

下図の様に同じ大きさの直方体を水の中に入れたと想像してください。
ただし、この直方体の質量は０で、直方体を水の中に入れると直方体内部にも水が入ります。
右側の直方体は水面から上面までがｈです。
上面と下面の面積をＳ、水の密度（単位体積あたりの質量）を ρ とします。

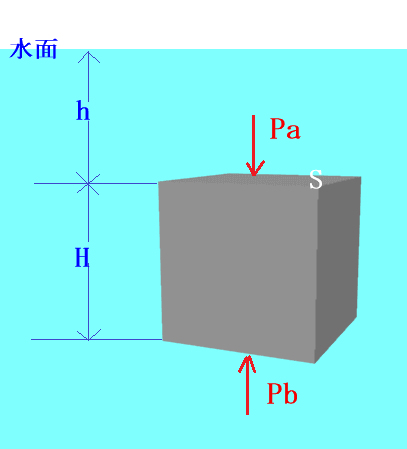
この直方体に掛かっている下向きの力 Pa を見つけます。
上面には、大気圧 S P0 と直方体の上面の水の質量 S h ρ g が下向きに掛かっています。
Pa=  P0 S + S h ρ g
ただし、この式では下向きの力であることを示す負号は付けていません。
下面には、下面を上から押す力と逆向きの力が上向きに働いてつり合っているので、
Pb = P0 S + S h ρ g + H S ρ g
下面を上に上げる力 Pb から上面を下に押す力 Pa を引くと
Pb - Pa = P0 S + S h ρ g + H S ρ g - (P0 S + S h ρ g )
Pb - Pa = H S ρ g
Pb -Pa が正なのでこの直方体には上向きの力が働き、その力の大きさは、体積（H S）分の水の質量に重力加速度 g を掛けたものです。
「体積が変化しない静止した流体内（たとえば水）の圧力は深さが同じなら何処も同じなので、流体内に入れた物の形には関係無く、その物が排除した流体の重心に掛かる重力と同じ大きさの浮力が生じます」　これがアルキメデスの原理です。

船が横転する理由とアルキメデスの原理

アルキメデスの原理で直ぐに思い浮かべるのが、ある物が水より重いか軽いかを確かめるにはその物を水に入れれば判るということです。
その物がどんなに複雑な課t値をしていても、また、秤が無くても、水より重ければ沈み、水より軽ければ浮くので一目瞭然です。
アルキメデスの原理の説明に使った直方体はその物の質量を考えなかったので水中に留まっていましたが、直方体の質量を考えて直方体が排除した水より重ければ沈みますし、軽ければ浮きます。
逆に、正確に体積と質量が測られた物を流体（たとえば水）に入れて沈むか浮くかを見れば、その流体の単位体積当たりの質量が判ります。自動車などに使われている鉛バッテリーの電解液の比重を測る比重計に利用されています。

さて、船にはアルキメデスの原理が利用されています。
下図１は船が傾いていない状態です。
船の中心線上に船の重力の重心と船が受ける浮力の重心があります。

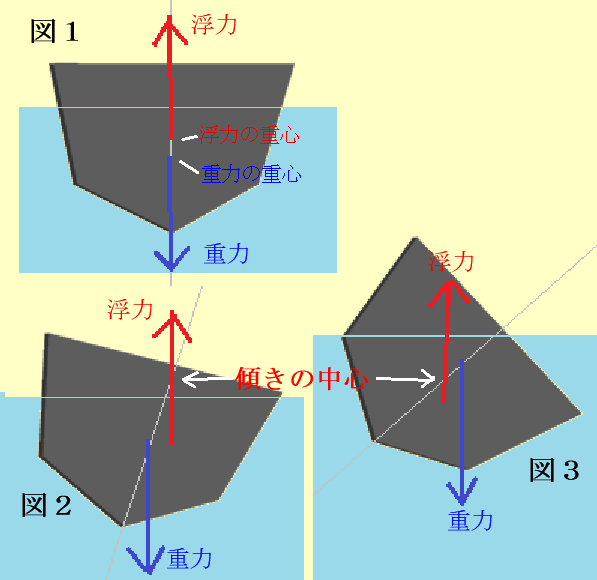
上の図２は、船が少し傾いた状態です。
船の重心は変わりませんが、船が傾くと船が排除した水の体積やその形が異なって来るので浮力の重心が移動します。
浮力の重心から浮力の方向に伸ばした直線と船の中心線が交わった点を傾きの中心と言います。
船が少し傾いた場合は、傾きの中心が船の重力の重心より上にあるので船の傾きが少なくなるように復元力が働きます。
ところが、船が大きく傾いた場合は、図３で示した様に、傾きの中心が船の重心より下にあるので、船は船自身の重力によって更に傾いてしまいます。
ですから、重心が高い船ほど傾きやすくなります。