摩擦係数とは? 摩擦係数を求める問題を解く
斜面上に置いた物体の摩擦係数
下図の様に水平な板Bの上に質量mの物体を置きました。
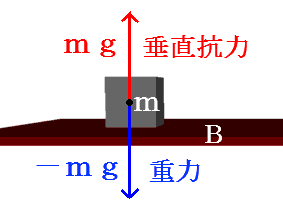
(gは重力加速度)
この時、上を正とすると、物体mには、-mgの重力が掛かっているのは直ぐに判りますが、物体mが板B上で落ちないで静止しているという事実から物体mには上に押し返す力mgが掛かっていることも判ります。この力を垂直抗力と言います。
垂直抗力と物体mに掛かっている力は向きが正反対だけで絶対値が同じですが、この二つの力は別物です。垂直抗力は板Bを構成する原子(分子)が押されて隣接する原子(分子)との間隔が狭くなってしまうのを元の間隔に戻そうとする力によります。
垂直抗力は物体mが板Bに加えた力の反作用で、物体mに掛かる重力は地球との間の万有引力によるものです。地球の作用反作用の法則の相手は物体mです。
次に、物体mを載せたまま板Bの左端を上げて θ 度傾けると、斜面上の物体mには下図で示した力が作用します。
滑り落ちる力や垂直抗力は、物体mに掛かる重力を平行四辺形を使った力の分解で計算出来ます。
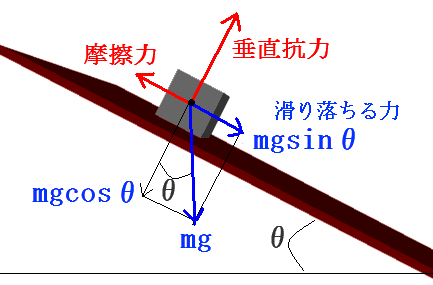
傾きθを大きくして行くと、物体mは滑り落ちます。滑り落ちる寸前に静止摩擦力は最大になります。
物体mが滑り落ちている時にも滑り落ちる運動を妨げる摩擦力が働きます、これを動摩擦力と言います。
摩擦力の大きさは、垂直抗力の大きさに比例することが判っています(経験則)
摩擦力=摩擦係数×垂直抗力
この時の物体mが滑り落ちているときの加速度は、距離を時間で2回微分すれば求められます。
先ず、運動方程式 質量×加速度=力という法則から、滑り落ちる物体mについて次式が成り立つ。
ただし、$μ$ は動摩擦係数
動いている物に載っている物体が動き出す瞬間の摩擦係数
トラックなどの荷台に物を載せて運ぶ時には物と荷台を結束しておかないと走行中に荷台から落ちることがあります。
荷台に載せた物が落ちるのは、物はそこに留まろうとしているのに荷台が動くからです。
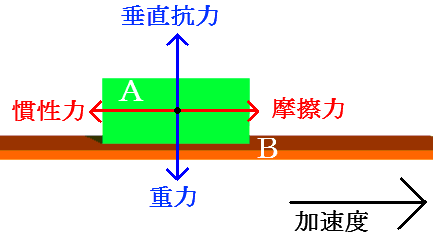
板Bの上の物Aの質量を$m$、重力加速度を$g$、物と板の間の静止摩擦係数を $μ$ 、加速度を$α$ として
板Bに対して物Aが滑り出す瞬間では静止摩擦係数が最大になり、
重力は、$mg$
垂直抗力は、物Aには重力しか掛かっていないので$mg$
摩擦力は、垂直抗力に摩擦係数を掛けたものなので $μmg$
慣性力は、運動方程式から$αmg$
となり、物Aが板Bに対して動き出す瞬間は、物Aは板Bに対して静止しているので慣性力と摩擦力の和は0になりますから、右方向を正にとれば、
$μmg+αmg=0$
ゆえに
$α=μ$ となります。