人力エレベーターの物理の問題
板の上に乗った人が滑車で吊ってその板を引き上げることができるのでしょうか?
引き上げる人自身が載った板を引き上げることが出来れば人力エレベーターが出来そうですが、自分の体重を引き上げる力が必要ではないか?と予測できますね。
考える人力エレベーターのイメージは下の様なものです。ロープ1本ではバランスが取れないだろうという突っ込みは入れないでください。
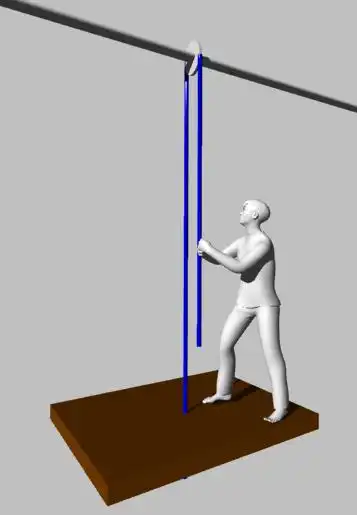
ロープの重さは無し、滑車の摩擦などが無いものとしてこの人力エレベーターの力関係を図示すると下図になります。
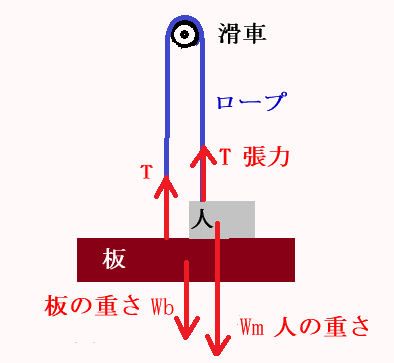
人と板の間には垂直抗力がありますが、人が板の上に載っている状態ではつり合っているので省いています。
重さが無いロープの両端では張力は等しくなりますから、ロープが板を引っ張る力と板の上に載った人がロープに引っ張られる力(ロープを引っ張る力)は同じになります。
では、条件から式を組み立ててみましょう。
先ず、人は板の上に載っている状態から、人を上に引っ張るロープの張力$T$は人の重さ$w_{m}$と等しいから小さくなければなりません。
先ず、人は板の上に載っている状態から、人を上に引っ張るロープの張力$T$は人の重さ$w_{m}$と等しいから小さくなければなりません。
$$w_{m}\geqq T \tag{1}$$
次に、板とその上に載った人が上に引き上げられるには、人と板の重さの合計よりロープの張力が大きくなければなりません。 $$T+T \geqq w_{m}+w_{b}$$ $$2T \geqq w_{m}+w_{b}\tag{2}$$ $$T=\frac{w_{m}+w_{b}}{2} \tag{3}$$
式3から人がロープを引く力は、人の重さと板の重さの和の半分以上が必要です。 式1の両辺を2倍して $$2w_{m}\geqq 2T \tag{4}$$ 式2と式4から $$2w_{m}\geqq 2T \geqq w_{m}+w_{b} \tag{5}$$ 式5から $$w_{m}\geqq w_{b} \tag{6}$$
式6から板の重さは人の重さ以下で無ければなりません。