このページは数式を多く使っているために完全な表示まで少し時間が掛かることがあります

2023/03/24作成

ニュートンの運動法則の説明からロケットが飛ぶ原理まで

ニュートンの運動法則と言われるものは、次の３つです

第一法則：慣性の法則
物体に外から力が加えられなければ、静止している物体は静止続け、動いている物体は速度と方向を変えずにそのまま動き続ける
第二法則：運動方程式
物体（質量$m$）に外から力$\vec{f}$が加えられると、物体には加えられた力に比例した加速度$\vec{α}$が生じて、速度と方向を変える
$\vec{ f }=m\vec{α}$
力と加速度には大きさの他に向きがあるのでベクトルです、それを表すために$f$と$α$の上に矢印を付けていますが、ゴシック体で表したり、分かり切って居ることなので省力することがあります。なお、ニュートンが１６８７年に著したプリンピキア（自然哲学の数学的原理）では数式で説明していません
第三法則：作用反作用の法則
物体Aが物体Bに力を加える（作用）と、物体Bは加えられた力の大きさと等しく向きが正反対の力を物体Aに必ず加える（反作用）

では、ニュートンの運動法則を初めて知った初心者にも理解しやすいように要点を説明しましょう。

慣性の法則（law of intertia）

たとえば、机の上の硬貨（コイン）は指ではじくとかして力を加えなければ動きません。では、硬貨を指ではじいてみます。指ではじかれた硬貨は力を受けたので机の上を滑って動き出します。しかし、硬貨は慣性の法則に反して直ぐに止まってしまいます。止まってしまう理由は、硬貨と机の接触面で硬貨が動く方向とは正反対の向きに摩擦力が、その上に空気抵抗が働くからです。ですから、摩擦力ゼロで空気抵抗ゼロ、硬貨の動きを妨げる力が外部から加えられなければ、硬貨は慣性の法則どおり永久に動き続けます。
慣性というのは、外部から力を加えない限り今の運動状態を維持し続ける性質です。

しかし、運動法則の１番目として提示された慣性の法則にはもっと深い意味があります。
真っ暗で観測者には机の上の硬貨だけが見えるとして、観測者が気づかないまま観測者が動かされたらどうでしょうか？
硬貨が静止しているものと思わなければ、観測者が動いたのにも関わらず硬貨が動いたと見えます。
要するに、慣性は物体が持つ性質では無くて、観測者によって違うものということです。
そこで、次に続きます

慣性系とは何か？

物体に力を作用させないかぎり（力を加えない限り）、その物体の運動状態が変化しない世界（座標系）が慣性系です。
ときどき、電車の車内の床上に缶ジュースなどの空き缶が転がっていることがありますが、電車が動き出したり止まったりすると今まで動かなかった空き缶が転がり出します。
この現象は、電車を基準点にした座標系では慣性系の世界で起きたものではありません。
なぜなら、座標系の基準点は電車ですから電車が動くとか止まるということは無いので、何の力も作用していないのに空き缶が転がり出すからです。
しかし、これでは空き缶が転がり出す説明が出来ないので、座標系の基準点を電車の外の地面に移せば、電車が動き出したので、または電車が止まったので、空き缶が動き出したと説明出来るので慣性系になります。
ということで、運動法則の第２と第３は、慣性の法則が成り立つ慣性系内の話です、と続きます。

運動方程式（equation of motion）

運動方程式は

$$\vec{ f }=m\vec{α} \tag{1}$$

というように、力と加速度の関係で表されることが多いですが、ニュートンは運動量に着目していました。
物体に力を加えないときは$f=0$なので、運動方程式
$0=m\vec{α} $を成り立たせるには$\vec{α}=0$になる必要があります。
加速度は速度の変化量で、速度$v$を時間$t$で微分したものです。速度に変化が無ければ時間で微分した結果はゼロになります。
ということで、力を加えないと加速度（速度の変化量）がゼロ、静止している物はそのまま静止続け、動いている物は速度と向きを変えずに動き続けます。これは運動の第一法則の「慣性の法則」を言っています。

次に、運動方程式を加速度$\vec{α}$に注目して

$$\vec{α}=\frac{\vec{f}} {m}$$

とすると、加速度$α$は、同じ大きさの力$\vec{f}$ならば質量$m$が大きいほど小さくなることが解ります。日常の経験でも、軽い物は容易に動かせますが重い物を動かすのは大変です（重い物はそれが置かれた物との接触面での摩擦力が軽い物より一般に大きくなりますが、摩擦力が無い状態でも重い物は動かし難いです）
物体の質量は、力に抵抗して慣性を保とうと働きます。そこで、慣性質量と呼びます。

ところで、運動方程式$\vec{ f }=m\vec{α} $は、力の単位$N$（ニュートン）を定義しています。
すなわち、１$N$は質量１$kg$の物体に作用して１$m/s^{2}$の加速度を生じさせる力の大きさです。
地球上では、たとえば筋トレをしようとしてバーベルを持ち上げただけで手腕に力が加わります。質量１ｋｇのバーベルなら、地球上の重力加速度は約９．８$m/s^{2}$なので$[１ｋｇ]・９．８[m/s^{2}]N$となりますから、手腕に掛かる力の大きさは９．８Nとなります。
日常生活で、体重６０ｋｇなどと言うときは「重さ（重量）」ですが、これは（質量×と重力加速度）になっています。質量と重さを同じように扱っていますが、正確には６０ｋｇｗです。重力が地球の約６分の１の月で体重計で測れば目盛りは地球上で測った６分の１になりますが、質量は地球でも月でも同じです。ちょっと高級な秤には重力加速度を補正するために秤を使用する地域を選べるようになっているものがありますが、６分の１まで重力加速度を補正出来る体重計で測れば月でも地球上と同じ値を示します。

ニュートンは運動量に着目して運動方程式を考えていました

ニュートンが提示した運動方程式は
物体が持つ運動量の変化率は、その物体が受ける力に等しい

$$\vec{f}=\frac{d\vec{p}}{dt} \tag{2}$$

ただし、運動量$\vec{p}=m\vec{v}$

というものです。
運動量は、質量$m$×速度$\vec{v}$で表されますが、速度には方向があるので運動量はベクトルになります。
ニュートンが運動量に着目した運動方程式を提示したのは、運動量が物体の運動を記述する基本量だからで、高速で動く物体についてもこの型の運動方程式は成り立ちます。
物体に力が加えられていないとき$f=0$ならば、

$$0=\frac{d\vec{p}}{dt}$$

となりますから、物体が持っている運動量は保存されます
また、ロケットや雨滴の様に運動中に物体の質量が変わるようなものでも記述が簡単になる利点があります。（ロケットは燃料を消費しながら飛ぶので徐々に質量が小さくなります。雨滴は、周囲の小さな雨滴を吸収しながら落ちるので質量が大きくなります、質量が大きくなるので上昇気流に乗れずに落ちます。地上近くなると空気が幾分乾燥してくるので雨滴の水分が気化して質量が小さくなりながら落下します）

運動量で表した運動方程式は、

$$\vec{f}=\frac{d\vec{p}}{dt} = \frac{dm\vec{v}}{dt} = m\frac{d{\vec{v}}}{dt} = m\vec{α} \tag{3}$$

となり、私たちが良く知っている加速度を使った運動方程式と同じものだと判ります。

作用反作用を理解するのに助けになる「力積」を説明して起きます

力積$\vec{I}$とは、文字通り力$\vec{f(t)}$を時間$t_{1}$から時間$t_{2}$まで積み重ねたものです。数式で書くと

$$\vec{I}=\int_{{t}_{1}}^{{t}_{2}}\vec{f(t)}dt$$

運動量$\vec{p}$に着目した運動方程式によると

$$\vec{f}=\frac{d\vec{p}}{dt} \tag{4}$$

なので、力と運動量が時間で変化すると考えて、式（４）の両辺を時間$t_{1}$から時間$t_{2}$まで積分すると

$$\int_{{t}_{1}}^{{t}_{2}}\vec{f}(t)dt= \int_{{t}_{1}}^{{t}_{2}}\frac{\vec{p}(t)}{dt}dt$$

ゆえに、力積と運動量の関係は

$$\int_{{t}_{1}}^{{t}_{2}}\vec{f}(t)dt= \vec{p}({t}_{2}) - \vec{p}({t}_{1}) \tag{5}$$

となります。

以降、ベクトルを表す矢印を省力します

作用反作用の法則

物体を押したら同じ大きさの力で押し返されるという法則は、手で机を叩いたら手が痛い、と簡単に説明出来ますが、この作用反作用は意外に奥深い法則です。
ニュートンが運動方程式を運動量を使って表したのは運動量が物体の運動を記述する基本量だからですが、運動量の恩恵を受ける例としてロケットが飛ぶ理由を説明したいと思います。その前に

二つの物体の間にだけ力が作用している場合は運動量が保存されるという法則を導いてみます

物体Aが物体Bに対して時間$t_{1}$から$t_{2}$まで$f_{a}(t)$という力を作用させると、式（５）を利用して

$$力積I_{a}=\int_{t_{1}}^{t_{2}} f_{a}(t)dt=p_{a}(t_{2})-p_{a}(t_{1}) \tag{6}$$

作用反作用の法則により、物体Bから物体Aに対して作用する力を$f_{b}(t)$として

$$力積I_{b}=\int_{t_{1}}^{t_{2}} f_{b}(t)dt=p_{b}(t_{2})-p_{b}(t_{1}) \tag{７}$$

作用反作用の法則により$f_{a}(t)=－f_{b}(t)$なので

$$I_{a}+I_{b}=\int_{t_{1}}^{t_{2}} (f_{a}(t)+f_{b}(t))dt=0$$

ゆえに、式（６）と式（７）の力積と運動量で表した部分を足すと、

$$I_{a}+I_{b}=p_{a}(t_{2})-p_{a}(t_{1}) + p_{b}(t_{2})-p_{b}(t_{1}) =0 \tag{8}$$

時刻$t_{1}$と時刻$t_{2}$で物体Aと物体Bが持つ運動量の和に変化があったか確認するために式（８）から

$$p_{a}(t_{1})+p_{b}(t_{1}) = p_{a}(t_{2})+ p_{b}(t_{2}) \tag{9}$$

となって、物体Aと物体Bの運動量の和は、変化しないで保存されることが判りました。

ロケットが飛ぶ理由

説明を簡単にするために、外力（天体からの引力）が掛からない宇宙空間をロケットは飛んでいるものとします。
エンジンを点火しない状態のロケットの全質量を$m+Δm$、速度を$v$とします。
エンジンを点火して、質量$Δm$の物体（実際は燃焼ガスですが）をロケットから見て速度$u$でロケットの進行方向とは正反対の方向に噴射しました。
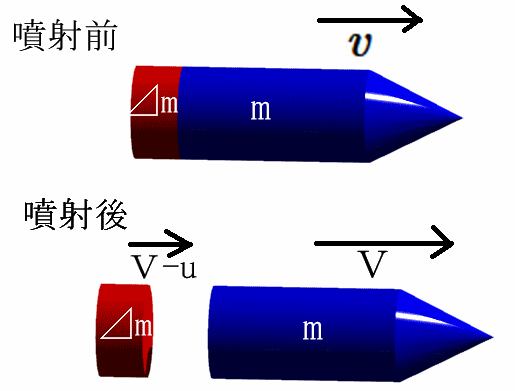
ロケットが飛ぶ原理説明図

ここで、ロケットがエンジンを点火する前の運動量と点火して質量$Δm$のガスを噴射した後の運動量を求めます。
運動量は質量に速度を掛けたものですから
ガス噴射前にロケットが持つ運動量は、$(m+Δm)v$
ガス噴射後にロケットが持つ運動量は、$mV$　ただし、$V$は噴射後のロケットの速度
ガス噴射後に噴射されたガスが持つ運動量は、$Δm(V-u)$
外部からの力は作用していないので噴射前と噴射後の運動エネルギー量は保存されるから

$$(m+Δm)v = mV + Δm(V-u) \tag{10}$$

式（１０）の左辺が噴射前の運動エネルギー、右辺が噴射後の運動エネルギー
式（１０）から噴射後の速度$V$を求めると

$$V = v +\frac{Δm}{m+Δm}u \tag{11}$$

となり、質量のある物を速く噴射するほどロケットの速度が増すことがわかります