仕事とは 例題で易しく説明
「仕事」と言っても、サラーリマンとか農業というのでは勿論ありませんが、物を運んだり、何かする、という仕事に近いです
物理では、物体に力$F$を働かせ、その物体が$s$だけ動いたときに、力$F$と動いた変位$s$の積$Fs$を仕事$W$と言います。 $$ W = Fs$$ 力$F$の単位はニュートン$N$、変位$s$の単位はメートル$m$なので、力$F$の単位は$Ns$となり、$Ns$をジュール$J$としています。
ですから、$1N$の力で$1m$動かしたときの仕事$W$は$1Ns$で$1J$となります。
注意することは、力は変位の方向と同じ方向を持つということです。
ただし、力を加えたら力とは正反対の方向に変位する場合があります。このときは、仕事量は負の値になります。
物体が斜面を滑り落ちるときの仕事を求める
角度$θ$の滑らかでは無い斜面から質量$m$の物体が距離$s$だけ滑り落ちたときの仕事を求めてみます。
“仕事”というと人や機械がすると思ってしまいますが、力が働けば仕事になります。
斜面を滑り落ちている時に物体に作用している力を表したのが下図になります。
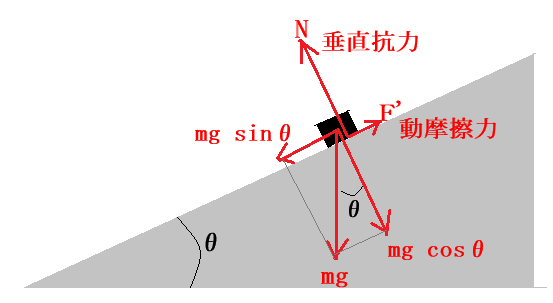
先ず、重力が物体が変位に作用している力は斜面に平行な成分なので$mg \sin(θ)$、変位は$s$ですから、重力がする仕事$W_{g}$は$mg \sin(θ)s$になります。ただし、$g$は重力定数
次に、垂直抗力$N$がする仕事は、垂直抗力$N$が変位方向に垂直なので仕事は$0$です。
動摩擦力$F'$がする仕事は、動摩擦力$F'$が変位方向とは正反対の向きになるのでマイナスが付いて、動摩擦力がする仕事$W_{k}$は$-F's$になります。
したがって、物体に働く力がする仕事は
倒れている円柱を垂直にするときの仕事を求める
下図の様な、直径$2r$、長さ$2l$、質量$m$、均質な円柱の場合は、
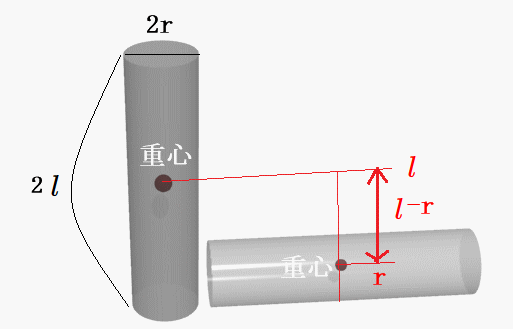
この問題は、円柱の重心の高さの変化に着目します。
というのは、たとえば、水を10mの高さから落として回す水車を作って仕事をさせるとします。
この水車を回すための水を、10mの高さまで電動の水ポンプで上げたても、人が水を入れたバケツを持って梯子を上って上げても、水車の回り方は全く同じで、水車がする仕事も同じです。
この様に重力を使う仕事は、始めの位置と終わりの位置だけを見ればその間は関係無いのです。このような力を「保存力」と言います。
保存力は、位置エネルギーを持ち、外部と遮断されていればエネルギーが保存されるので保存力と言います。
円柱を立てたときの重心の高さは、円柱の長さの半分、すなわち、$l$です。
重力加速度を$g$とすれば、力は$mg$、変位は$l-r$。よって、仕事$W$は $$W = mg(l-r)$$ となります。
高さの位置エネルギーですね。
前の斜面の問題も、摩擦力が無ければ、式1は
軸の周りを回っている物の仕事
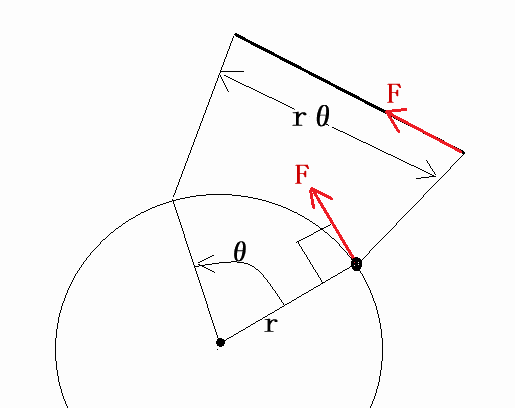
接線方向に働く力$F$によって物が接線方向に変位するので、結局のところ、力の方向と変位の方向が同じ直線上にあるのと同じで、仕事$W$は
物体を回転させようとする力であるモーメント(トルク)は、接線方向の力とその力が作用する点と回転軸からの距離の積なので、トルク$N$は$Fr$
式2は $$W = Nθ$$ 回転する物の仕事は、トルクと回転角の積で表されます