夜が暗い理由
夜が暗い理由を問われれば、太陽が沈んでしまう、星の光は少ないと答えるのが普通だと思います。古代から昼間は太陽が創ると考えられていましたから。 例えば、ギリシア神話では太陽神アポロンが光球を積んだ車を東から西に運んでいる間が昼間ですし、日本神話では太陽神天照大神が隠れてしまうと夜になります。
ところが夜が暗いのは太陽には関係ありません。 木々が生い茂った森の中に居ると、どの方向を見ても隙間無く木しか見えません。これと同じ様に宇宙に無限に太陽の様に自ら光を放つ星が存在するなら星しか見えないのですから夜も明るいはずです。「夜が暗い理由」の答えが出たのは、1960年代になってからです。
簡単な計算で夜が暗い理由が太陽に関係無いことを説明してみます
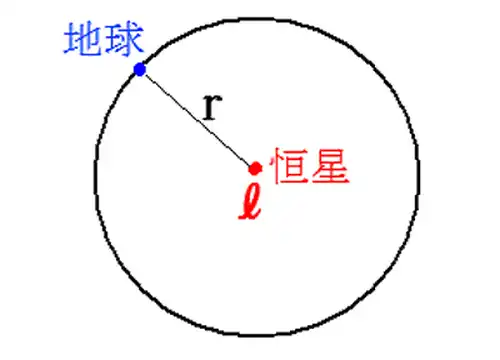
地球から距離$r$の点にある星から地球に届く単位面積あたりの光量$L$は、星からの光は四方八方に均一に放射されるので球体の表面積の公式を使って
但し、$π$は円周率。
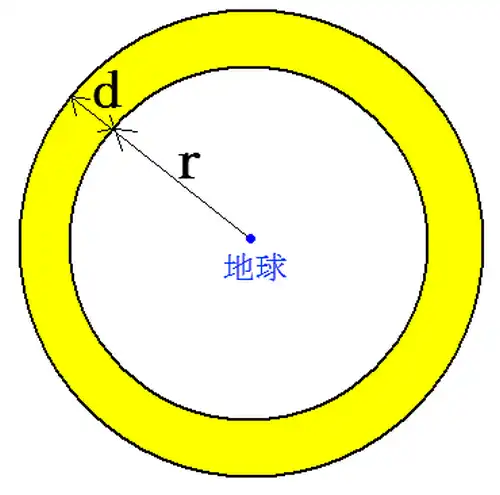
単位体積あたりの星の数(密度)は$n$と仮定しているので、半径 $(r+d)$の球の体積から半径$r$の球の体積を引いたものに$n$を乗ずれば星の数は求まりますが、ここでは地球から無限の距離にある星の数を求める都合があるので、$d$を極小さい区間として求める星のある体積部分$V$を球面の面積×$d$ として
次に地球から半径$R$までにある全ての星から地球に降り注ぐ光の合計$W$を求めます。これには式2を$0$から$R$まで積分すればよいので $$W=Rnl \tag{3} $$ となります。(式2の$d$は積分の式に出てくる微小区間で定積分をしています)
ここで、星は無限にあると仮定していることを思い出すと、地球に降り注ぐ光の合計は$R$を無限大にすることと同じなります。なぜなら、宇宙空間が有限ならそこにある星の数も有限になってしまうからです。
式3の$R$を無限大にすると地球に降り注ぐ光も無限大になってしまい、夜が明るいのを通り越して地球が焼き尽されてしまいます。実際には夜は暗い訳ですから計算結果と矛盾します。
オルバース(H.W.M.Olbers 1758-1840)が1826年に発表したので「 オルバースのパラドックス (1826)」と呼びます。
オルバースの間違い
この計算におかしい部分があるのでしょうか・・・
天の川を見たことのある方なら、オルバースが仮定した、“宇宙は無限で星が一様に分布している”というのがおかしいと気付くと思います。しかし、当時の宇宙像は星が一様に分布しているというのが一般的で、この宇宙像を提唱したニュートン(Isaac Newton 1642-1727) が偉大な学者だった為にそのまま受け入れられていたようです。しかし、宇宙が無限か? という問題はニュートンが生まれる前に、ケプラー(Johannes Keple 1571-1630) が1610年に「宇宙が無限で太陽と同じような星が一様に分布していたら星の明るさで太陽が凌駕されしまうから宇宙は無限では無い」と結論付けています。ケプラーよりニュートンの宇宙像が評価されていたのは、ケプラーが一介の貧乏学者に過ぎなかったからでしょうか。
話は戻りますが、「天の川や多くの銀河が宇宙にあって星は一様に分布していない」という事になっても、オルバースのパラドックスは解明されませんでした。なぜなら、星の代わりに銀河を考えて、銀河が宇宙に一様に分布すると考えれば、空は銀河の光で明るくなるはずだとなるからです。結局のところ、星や銀河が一様に分布するかどうかを考えるのは徒労の様な気がします。また、宇宙に一様に星が分布していて宇宙の大きさが無限であってもその無限の星の光が全て地球に届く訳ではありません。 というのは、霧が出て100m先しか見えない状況を考えてみてください。100m先からその先1km霧が続いても10km続いても、前方の霧粒がその後方にある霧粒を遮ってしまう為に100m先しか見え無い事に変わりが無いのと同じです。(地球から見て前方にある星が後方にある星を遮る)
宇宙の場合は、霧粒を星と考えて星の大きさから計算すると、150億光年先の星は前方の星に遮られて見えなくなるそうです。
さて、これまでの話では、光の速度や星の寿命に触れませんでしたが、オルバースのパラドックスは星が放つ光は距離に関係無く一瞬で届き、且つ星の命は永久に続くと言う仮定で成り立っています。しかし、周知の通り、光の速度は有限です。(オルバースが生まれる83年前に発見されています)ですから、遠くの星(または銀河)の光はまだ地球に届かない、近くの星は寿命が来て燃え尽くしてしまったと考えれば、全ての星の光は届きませんから夜の空が暗くてもよい訳です。
夜が暗い理由の明快な答え
これで一応解決したようなのですが、もっと明快な答えがあります。スライファー(V. M. Slipher 1875-1969) は25個の銀河(当時は渦巻星雲)の光を観測して、その光が赤い方にずれている(赤方偏移)と1914年発表しました。
光が赤方偏移するのはドップラー効果 によって銀河が遠ざかっているからで、ハップル(Edwin Powell Hubble 1889-1953) は「銀河の後退速度は、その銀河までの距離に比例する 」という法則を確立しました。
⇒ 近づいてくる音が高くなるドップラー効果が起きる理由
ハップルの法則に拠れば、遠くにある銀河ほど速いスピードで遠ざかってしまうのですから、有限速度を持つ光では地球に届くことは無く夜の空は暗いようです。