当ページと関連する話題
外積の計算方法
外積の計算方法の前に、簡単に計算できる内積から説明します内積の計算方法
デカルト座標系（x,y,zで位置を表す座標）、ベクトル $\mathbf{a}$ の成分を $(a_{x}\ a_{y} \ a_{z})$ 、
ベクトル $\mathbf{b}$ の成分を $(b_{x}\ b_{y} \ b_{z})$ とすると、内積は
$$\mathbf{a}\cdot\mathbf{b}=a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}\tag{1}$$
で表されます。
この式の求め方は、ベクトルの内積と外積で説明していますから興味のある方は参照してください。
$\mathbf{a}=(2,1,3)$、$\mathbf{b}=(1,-1,1)$ なら、先に示した式１にそのまま代入して
$$\mathbf{a}\cdot\mathbf{b}=2\times1+1\times(-1)+3\times1=4$$
外積の計算方法
外積の計算は内積の計算よりはるかに面倒です。
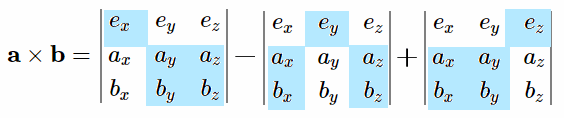
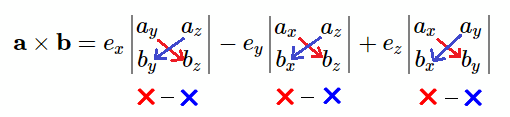
計算式は、複雑なので次の行列式で覚える方が簡単です。
$$\mathbf{a}\times\mathbf{b}=\begin{vmatrix}e_{x} & e_{y} & e_{z}\\a_{x} & a_{y} & a_{z}\\
b_{x} & b_{y} & b_{z}\end{vmatrix}\tag{2}$$
$e_{x}\ e_{y}\ e_{z}$ は単位ベクトルです。
式２からは機械的に下図の水色で塗られた順に行列式を展開して行きます。
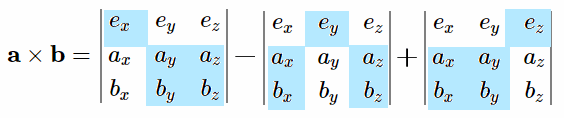
$$\mathbf{a}\times\mathbf{b}=e_{x}\begin{vmatrix}a_{y}&a_{z}\\b_{y}&b_{z}\end{vmatrix}
-e_{y}\begin{vmatrix}a_{x}&a_{z}\\b_{x}&b_{z}\end{vmatrix}
+e_{z}\begin{vmatrix}a_{x}&a_{y}\\b_{x}&b_{y}\end{vmatrix}$$
$$=e_{x}(a_{y}b_{z}-a_{z}b_{y})-e_{y}(a_{x}b_{z}-a_{z}b_{x})+e_{z}(a_{x}b_{y}-a_{y}b_{x})\tag{3}$$
式３の展開は、下図で示した様に、赤い矢印で結んだものを乗じたものから青い矢印で結んだものを乗じたものを引きます。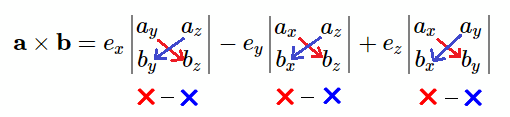
$\mathbf{a}=(2,-1,3)$、$\mathbf{b}=(1,4,1)$ の外積は式３に代入して
$$\mathbf{a}\times\mathbf{b}=\begin{vmatrix}e_{x} & e_{y} & e_{z}\\ 2 & -1 & 3\\ 1 & 4& 1 \end{vmatrix}$$
$$=e_{x}\begin{vmatrix}-1&3\\4&1\end{vmatrix}
-e_{y}\begin{vmatrix}2&3\\1&1\end{vmatrix}
+e_{z}\begin{vmatrix}2&-1\\1&4\end{vmatrix}$$
$$=e_{x}(-1\times1-3\times4)-e_{y}(2\times1-3\times1)+e_{z}(2\times4-(-1)\times1)$$
$$=-13e_{x}+e_{y}+9e_{z}\tag{4}$$
$e_{x}\ e_{y}\ e_{z}$ は基本ベクトルなので、求められた外積はベクトルです。そして、基本ベクトルを $\mathbf{1}$ とすれば、式３の答えは $\mathbf{a}\times\mathbf{b}=(-13,1,9)$ という表記にも出来ます。