＊数式が多いために正常に表示されるまで時間が掛かる場合があります。

荷台に載せた物が滑って動いてしまう理由運動の法則と摩擦の問題

自動車のダッシュボードの上にスマホを置いたまま走り出すとスマートホンが滑り落ちてしまうことがあります。

ダッシュボードは運転時の視界を妨げないように物が起きずらい形や表面仕上げになっているのでしょうが、例えば、下図の様に平ボディのトラックの荷台に箱を荷台に留めずに置いてもトラックが動き出せば箱が荷台上を滑って動くことがありますし、動かないこともあります。
荷台に置いた箱が重ければ重いほど動かないのでは？トラックがゆっくり動き出せば動かないのでは？　と思いますが、どのくらい重ければ箱は動かないのでしょうか？　どのくらいゆっくり動き出せば箱は動かないのでしょうか？

広い荷台に小さな箱でしたら動いても落ちることは無いだろうと思いますが、JR貨物のコンテナーを積んだ大型トラックを見掛けたときは落ちないものだと思ってしまいます。

上図の平ボディのトラックの荷台に箱を置いた問題を簡単にするために箱を載せた荷台が箱と一体になって滑らかな水平な平面上を力$F$で直線上を左に動き、空気の抵抗は無いものとします。
箱の質量を$m$、荷台の質量を$M$、荷台と箱の間の静止摩擦係数を$μ_{0}$、重力加速度を$g$とします
（摩擦係数については摩擦係数とは？摩擦係数を求める問題を解く）
この時に働いている力は下図の様になります。

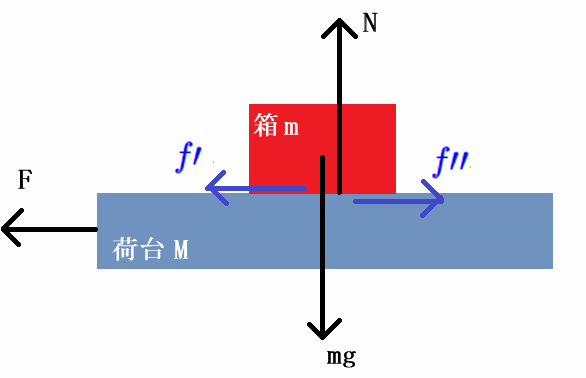
$N$は垂直抗力で$N=mg$です。垂直抗力は荷台の上面から箱の下面に掛かっているもので、垂直抗力が無ければ箱は落ちてしまいます。垂直抗力は原子や分子の間に働いている電気によるものです。
荷台と箱が接している部分には静止摩擦力が働いています。摩擦力が働いていなければ荷台が動いても箱は動きません。
荷台に働く静止摩擦力は荷台の動きを妨げる向きに働くので図の$f\prime\prime$、箱に働く静止摩擦力は箱が静止しているのを妨げる向きなので図の$f\prime$になります

次に、ニュートンの運動法則の２番目の運動方程式[力＝質量×加速度]を使って、箱についての運動方程式は

$$f\prime=mα_{1} \tag{1}$$

荷台についての運動方程式は

$$F-f\prime\prime=Mα_{2} \tag{2}$$

ただし、$α_{1}$は箱の加速度、$α_{2}$は荷台の加速度
箱と荷台は一体で動いているので、静止摩擦力と加速度は向きが逆で大きさは等しいので

$f\prime=f\prime\prime$、$α_{1}=α_{2}$

$α=α_{1}=α_{2}$、$f=f\prime=f\prime\prime$と置き換えると、

式１は

$$f=mα \tag{3}$$

式２は

$$F-f=Mα \tag{4}$$

知りたいのは荷台に載せた箱が動き出す時の条件です。
箱が動くには最大静止摩擦力（$μ_{0}N$）より静止摩擦力$f$が大きい必要がありますから、先ず、式３と式４から$f$を導き出します。

$$F-f=M\frac{f}{m} \tag{5}$$

よって、

$$f=F\frac{m}{M+m} \tag{6}$$

箱が動くには$f > μ_{0}N$　で、$N=gm$　だから

$$F\frac{m}{M+m} > μ_{0}gm \tag{7}$$

$$F > μ_{0}(M+m)g \tag{8}$$

式８の条件を満たせば箱が動きます。

荷台に加える力$F$は、加速度と質量で表されますから、加速度$α$、質量$(M+m)$ で

$$(M+m)α > μ_{0}(M+m)g$$

$$α > μ_{0}g$$

となって、箱が動き出してしまう加速度$α$は、静止摩擦係数$μ_{0}$で決まることになります。静止摩擦係数$μ_{0}$が変わらければ、自動車の急発進や急停止時には加速度が大きくなるので、ダッシュボードの上に置いたスマホなどは動きやすく、最悪時にはダッシュボードから落ちてしまいます。
静止摩擦係数は、この場合では箱と荷台の接触面の状態で決まります。滑り止め用にゴムシートが売られていますが、このような物なら摩擦係数は大きくなります。
実際には、接触面の材質が同じでも箱が重ければ荷台との接触面の摩擦係数が大きくなることがありますし、風圧もありますから重い方が動きづらいです。

荷台に載せた物が滑って動いてしまう理由 運動の法則と摩擦の問題

荷台に載せた物が滑って動いてしまう理由運動の法則と摩擦の問題