ネジの仕組み・原理

“ネジ”と言うと自動車や電化製品、家屋等に使われているイメージが強い方が多いと思いますが、日に何度も目にする飲料や調味料が入っているペットボトルや瓶はネジによって蓋が締められています。

ネジはペットボトルや瓶の蓋の様に取り外しが必要だからというだけで使われているのではありません。
下図は、ネジを誇張して描いたイメージで、赤い四角の部分を取り出すと斜面と考えられます。

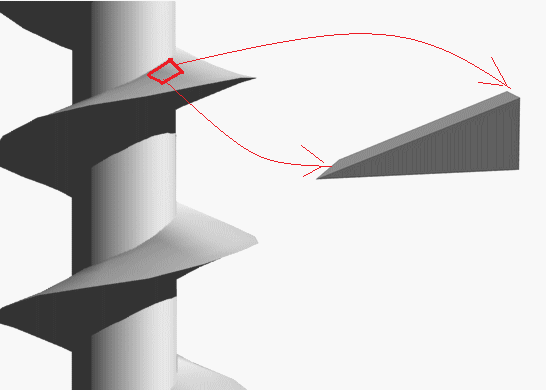
ここで、ネジの原理は斜面の原理というか“斜面の効用”の問題になりました。

斜面は、古くは古代エジプトのピラミッドの建造に利用されたと言われます。
ピラミッドは石を積んで造られていますが、クレーンといった重機が無かった時代に重い石を高い所に直接上げて積むのは困難です。
そこで、石のある所とその石を積む高い所まで斜面を作って斜面上を石を引きずり上げました。
斜面（スロープ）を使った方が、その斜面の角度が小さい方が楽なのは、たとえば、くねくね曲がりながら登って行く山岳道路や跨線橋などで経験上でも理解できますが、本当に楽なのかどうか簡単な計算をしてみましょう。

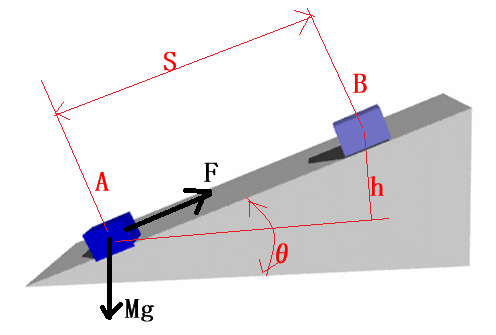
下図のように、角度$θ$の滑らかな斜面上を、質量$M$の物体をＡからＢに引き上げるために必要な力$F$を求めてみます。
ただし、$g$は重力加速度です。

滑り落ちる条件から求める方法

物体を引き上げる力$F$が無ければ、斜面と物体の間には摩擦力が無いので物体は滑り落ちてしまいます。そこで、滑り落ちる力$F'$を求め、その力より大きな力$F$で引き上げればよい訳です。
下図の様に書いてみると簡単で

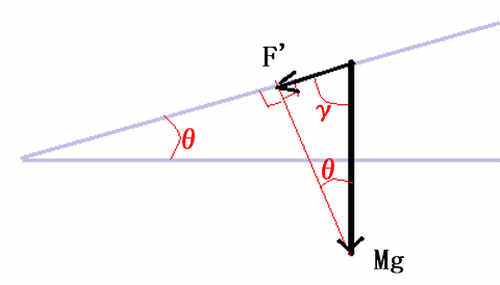
図より

$$F'= Mg \cos(γ)$$ $$γ=\pi -θ$$ $$F' = Mg \cos(\pi - θ) $$ $$= Mg \sin(θ)$$

ただし、$0<θ< \pi /2$
よって、$F'$より大きい$F$で引けば物体は斜面を登り、斜面の角度$θ$が小さいほど$Mg$より小さい力$F$で物体を上げられることになります。
自転車を漕いでいても緩い坂道の方が楽ですね（ただ、急な坂より長い距離登らなければなりませんが）

「仕事の原理」から求める方法

物体に力$F$を加えて物体の位置が$s$変化した時、力$F$と変位$s$の積$Fs$を、力$F$がした仕事と言います。
（⇒ 仕事とは　例題で易しく説明）
再掲ですが下図で、

力$F$が質量$M$の物体を斜面上の変位$s$（ＡからＢまで）まで斜面上を動かしたときの仕事$W$は$Fs$です。
斜面を使わずに持ち上げたときの仕事は、力は物体に掛かっている重力で$Mg$、変位は持ち上げる高さ$h$なので、仕事は$Mgh$になります。
「仕事の原理」から、物体を斜面を使って上げたときの仕事と直接持ち上げた仕事は等しいので

$$ Fs = Mgh $$ $$ F = Mg \frac{h}{s}$$ $$= Mg \arcsin(\frac{h}{s})$$ $$= Mg \sin(θ)$$

ただし、$0<θ< \pi /2$

ネジを使うメリット

ネジは斜面で構成されていて、上記で説明したように、ネジを回すとその斜面に接触している部分を押し上げます。 このときの押し上げる力は、ネジを回す力を一定とすればネジのピッチが小さいほど大きくなります。 ピッチと言うのは、ネジ山の間隔で、ピッチが小さいほど斜面の角度$θ$が小さくなります。
ネジが接触している部分を押すのが最もよく解るのは、木ネジです。
木ネジは木材に板などを留めるときに使いますが、ドライバーでネジを回しながら押し込んで行くと硬い木材にも簡単に入って行きます。
ペットボトルや瓶の蓋にネジを使えば、蓋を回す力より弱い力で蓋とペットボトルや瓶の口部分を押し付けるので液体を入れても零れ難くなります。
その他、柱と柱の間に棚を作ったりするときに使う“でっぱり棒”とか“支え棒”と言われる物も棒の中にあるネジを回すことによって柱と柱を強く押して落ちないようにしています。

ネジを利用した極め付けは、自動車のタイヤ交換で車体を上げたり、家屋の増改築時などに家屋を支えるときに使うジャッキです。
形はいろいろですが、下図のような物です。

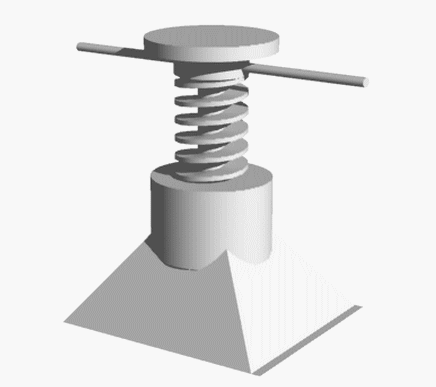
棒を回してネジを回して上面を上げて行きます。