バネばかりの作り方とフックの法則
更新これは非常に簡単な物です。
弾性のある物、たとえばバネを使って作ります。
学校にもあると思いますが、私はあまり好きな秤ではありません。
なぜって? 弾性が正確だと信じていないからです。経年劣化は勿論ですが。うっかり重い物を測ってしまったら弾性率が変わってしまうのでは?と心配症で
弾性というのは、外から加えた力で変形したものが、元の形に戻ろうとする性質を言います。
バネやゴムにその性質があります。
しなっていた釣竿が元に戻る力も弾性です。釣竿はバネですけど。
元の形に復元するものには「形状記憶合金」というものもありますが、これは外部から熱などを加えて戻るので重さを量る秤には使えません。
或る温度になったら知らせるというような、例えば火災報知器の自作には使えますが。
フックの法則
バネ秤は、バネが「フックの法則」と言われている物理法則に従う性質を利用しています。
フックの法則は「弾性限度以下では、バネの伸びとバネに加えている力が正比例する」というものです。 式で表すと、
$$F= - k x$$ 言葉で表すと
バネに加える力$F$は、$-1$×(それぞれのバネが持つ固有の定数$k$)× (バネが伸びた長さ$x$)
です。
フックの法則を表す式に$-$がつくのは、向きを考えているからです。
力$F$はバネに力を加えていない状態に戻ろうとする復元力なのでバネの伸びる方向(または縮む方向)とは逆の方向に働きます。 バネばかりを作るときの様にバネに加える力の方向とバネの復元力の方向を必要としない計算でよいなら右辺のマイナスを除いてフックの法則の式を $$F= k x$$ と表して差し支えありません。
バネの持つ固有定数をバネ定数といいます
複数のバネを直列や並列に接続したときのフックの法則は?
下図の様に2つのバネを並列に接続したときのフックの法則のバネ定数$k$は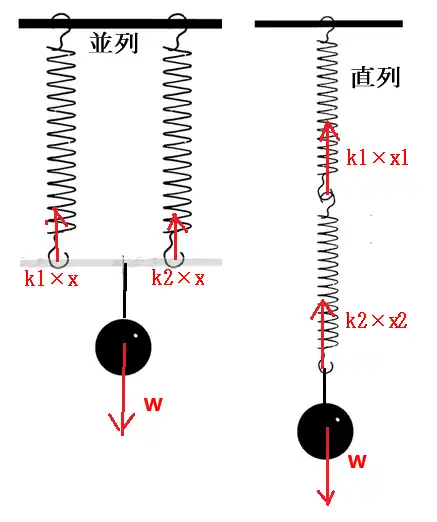
考え方は、バネの並列接続、直列接続ともに重りが重力で下に引かれる力とバネが元に戻ろうとする力がつりあっていることで考えます。
先ず、同じ長さでバネ定数が$k_{1}$と$k_{2}$のバネを並列に接続したときは(上図左)、 $$k_{1}x+k_{2}x = W \tag{1}$$ 式1の右辺の$W$は重りが重力で地球の中心に引かれる力です。重りの質量と重力加速度の積になります。この力は日常生活で“重さ”と言っているものです
ですから、重力加速度が異なれば式1での$W$の値も違ったものになります。
⇒ エレベーターに乗ったときに感じる浮く感じと床に押し付けられる感じの理由は、ニュートンの運動法則によるエレベーター内で体重計が増減する理由
ここで同じ質量の重りを1本のバネ(バネ定数$k$)が同じ$x$だけのびて釣り合っていると考えます
$$kx = W \tag{2}$$ 式1と式2は等しいので $$kx = k_{1}x + k_{2} x \tag{3}$$ ゆえに、同じ長さのバネを並列に接続したときのバネ定数は $$ k = k_{1} + k_{2}$$
バネ定数$k_{1}$と$k_{2}$のバネの直列接続は(上図左)、バネ定数$k_{1}$の上のバネが重りを支えていると考えて $$W= k_{1}x_{1} \tag{4}$$ ただし、下のバネの質量はゼロとしています。こういうところが、物理ですね。
下のバネも重りを支えているので $$W=k_{2} x_{2} \tag{5}$$ バネ2つの伸びた長さの合計$x$は $$x = x_{1} + x_{2} \tag{6}$$ バネ定数$k$の1つのバネで$x$伸びて重り$W$とつり合うと考えると $$ W = k x \tag{7}$$ 式4~式7からバネ定数$k$えお求めればよいので、式6右辺に式4と式5を代入して $$x=\frac{W}{k_{1}} + \frac{W}{k_{2}} \tag{8} $$ 式8の左辺に式7を代入して $$\frac{W}{k} = \frac{W}{k_{1}} + \frac{W}{k_{2}} \tag{9} $$ ゆえに、バネ定数$k_{1}$とバネ定数$k_{2}$を直列接続したときの合成バネ定数$k$は $$\frac{1}{k} = \frac{1}{k_{1}} + \frac{1}{k_{2}} \tag{9} $$
バネばかりを作る
伸び切ってしまったバネはもちろん、力を加えていないのに元の長さに戻らないバネはフックの法則に従いませんから秤には使えません。
秤の工作をしながら、フックの法則を確かめてみてください。フックの法則が使える範囲(重さとバネの伸びが比例する範囲)は広くはありません
さて、弾性が正確でなくても市販されているのは、作りが簡単なことと、1年に1度や2度は目盛りを較正するという期待からなのでしょう。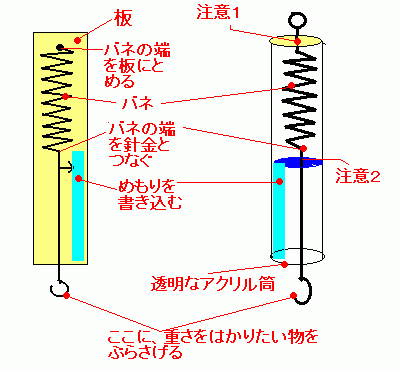
作り方は上図を見ればわかると思います。
右の図は透明なアクリル筒の中にバネを入れて、実用的にしています。
注意1 の部分は、アクリル板で筒の上部をふさぎ、そこにバネをとめています。
アクリルを接着するには、アクリル用接着剤というものが売られています。
注意2 の部分ですが、アクリル筒の中に楽に入る円形の紙を、バネと針金のつなぎ目部分にしっかりと接着剤で付けます。
この円盤がめもりの針になります。接着剤は合成ゴム系の工作用接着剤が良いでしょう。
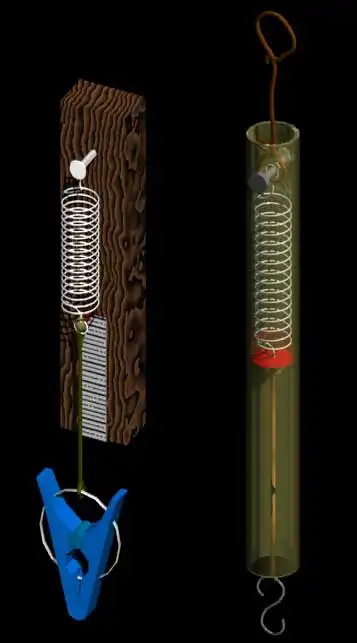
ハガキや封書などの郵便物の重さを測るのでしたら、上左の様に洗濯ばさみを付けるか、事務用のクリップを付けるのが簡単ですね。
バネの選び方ですが、重い物をはかろうとすれば、太くてなかなか伸びない物を、手紙のような軽い物しかはからないのなら簡単に伸びる小さな物を使います。
注意としては、バネはあまり伸ばし過ぎると始めの長さに戻らなくなるということです。
ですから、ハガキからキャベツまではかろうなんて考えないで、ハガキから封書までとか、野菜専用とかにしてバネを選んでください。
このバネ秤は量りたいものをぶら下げる型ですが、力を加えないときには伸びていて、力を加えると縮むバネなら量りたいものを上に載せる型になります。
望みのバネが入手できなくても、梃子や滑車を使って力の向きを変えれば、載せる型、ぶら下げる型になりますので研究してみてください。
下写真は、100円ショップのダイソーやセリアなどで100円+税で売られている簡易なキッチン秤(2022年5月時点)です。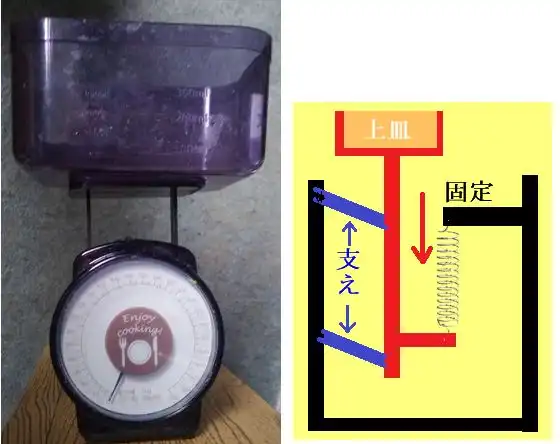
この秤は上の容器に量りたい物を入れて量るものですが、上図の右のような単純な方法でバネの伸びた長さで量っています。
製品では支えはバネがある方に付けられていますがごちゃごちゃしてしまうので図では反対側に描いています。
バネの伸びた長さを角度で示すには、直線運動を回転運動に変える歯車を使うのですが、この製品はもっと簡単な方法を使って居るようです。
上皿式の秤は便利ですが、可動部分を滑らかに動くようにする必要があるので難しいです。
材料がどこで売っているかですが、バネ、アクリル筒、アクリル用接着剤などほとんどの物は日曜大工用品、材料を売っている店(ホームセンターなど)で手に入りますが、バネ秤用というのは見たことはありません。
正確さを保証する校正が必要な秤を作ったり、自分で市販品を修理することは一般的ではありませんからね。
そこで、ホームセンター等で売られている一般用のバネを利用します。
下写真は、ホームセンターのカインズで2022年5月に見かけた「引きバネ」です。引きバネは、引っ張って使う伸びるバネです。
ラベルに「伸びる前の長さ、最大伸び長さ、最大荷重」が表示されているので、測りたい最大の重さから最大荷重、(最大伸び長さー伸びる前の長さ)がなるべく大きいバネを選びます。
(最大伸び長さー伸びる前の長さ)が大きい程、メモリを細かく刻めます。
バネばかりの目盛りの付け方
めもりの付け方ですが、何もぶらさげてない位置を0に書きます。
次に、重さのわかっている物をぶらさげて、バネが伸びて針が指した位置をその重さに書き込みます。
重さの判っている物としては“分銅”を使えば正確な目盛りが付けられますが、少々不正確ですが、重さが決まっている硬貨を使うと簡単です(1円硬貨1.0g 5円硬貨3.75g 10円硬貨4.5g 50円硬貨4.0g)
もっと重い物を測るバネばかりを作ったときは、たとえば、ペットボトルにぶら下げられるようにひもをつけ、 家庭にあるキッチン秤なので100グラムになるまでペットボトルに水を入れ、作ったはかりにぶらさげ、針が指した位置を100グラムとして書き込みます。
その次に、ペットボトルの水を増やして200グラムとして、繰り返します。
ペットボトルの重さだけ判れば、水1ccを約1gとしてペットボトルに入れる水量で水を入れたペットボトルの重さが判ります。
フックの法則が成り立つ範囲なら、バネが伸びる長さは重さに比例するので目盛りは均等になります。