重力加速度を簡単な方法で測ってみた&アインシュタインによる重力が生じる理由
更新日:
重力とは質量がある物質が地球に引かれる力です。 正確には、ニュートンの万有引力の法則で求められる「物と地球とに間に働く力」と地球の自転による遠心力とを合わせた遠隔力です。
ただし、遠心力は小さいので通常は無視しています。
二つの物体の間に働く引力は、それぞれの物体の質量 m1 と m2、そして距離 r の関数であることが示されました。
これを数式で表すと
ここで、Fは引力の大きさを表し、Gは万有引力定数です。
遠隔力というのは、普通の力が、車の衝突、槌で打つ、置くというように物と物が接触することによって生じるのに対して、重力は物と物とが接触しないでも生じているので「遠隔」が付きます。 林檎が落ちるときは林檎と地球は接触していませんし、太陽と地球の間や、地球と月の間も接触していないのに万有引力の式で示される力が働いています。
重力が生じる理由
ニュートンは、質量を持つ二つの物体間に働く引力(遠隔力)を求める式を表しましたが、アインシュタインはその力の根源を質量がある物は空間を歪めるからだと言います。
しばしばたとえられるのが環に張ったゴム膜の上に鉄球の様に重いものを載せた下図のようなものです。

中央の重い球によってゴム幕がロート状に変形するように空間が歪みます。この図は平面ですが空間は3次元なので想像力が豊かで無いとイメージがわきません。
私たちが住む地球が太陽の周りを回っているのも空間の歪みがあるからです。 地球よりはるかに質量がある太陽の周囲は空間が太陽に落ちるように歪んでいますから、地球は太陽目掛けて落下し、落下する力が太陽の周りを公転させています。
もしも、太陽に質量が変わるような大異変が起きると空間の歪みにも異変が起きて、空間の歪みが波のように伝わっていきます。これが重力波です。
空間が歪むことによって私たちが力と呼ぶものが働くことが理解しやすいのは、潮の満ち引きが起きる理由です。 この詳細は潮汐力・潮の満ち引きが起きる理由と大潮小潮とは何か?をご覧ください。
質量持つ物体間に働く重力が普通の力と異なるのは、遠隔で働くという以外に、重力には磁力や電気力にある反発し合う斥力が無いことです。 そのために、空間の歪みが伝搬する重力波は邪魔されずに伝わります。
重力の問題では「無重力」や「無重力状態」があります。国際宇宙ステーションや人工衛星の中は無重力だと言います。 また、無重力を体験するために飛行機のエンジンを切り滑空もしないで落ちることをします。
宇宙ステーションなどは地球に向かって落ちることによって地球の周りを回っていますし、エンジンを切った飛行機は直ぐに地面に激突します。 地球の引っ張られている重力があるのに無重力とは、ここが迷うところです。この問題については、 重さに関係無く同じ速度で落ちる理由と、落下する時に無重力になる理由を簡単に説明をご覧ください
宇宙ステーションに搭乗できる方は居無いでしょうし、エンジンを切って落下する飛行機もエンジンが掛からなかったらと思うと恐いものですが、 身近に重力の増減を体験できるのは高層マンションや商業ビルなどには必ずあるエレベーターです。 エレベーターでの上昇し始めと下降し始めの違和感が重力の変化で、事実、体重が増減します。
アインシュタインによれば、重力は変化するものです。ですから、エレベーター内で体重を測り、体重計の指示値が増減してもその値は正しいのです。 質量は変化しませんが、重さ(体重)は質量と重力加速度の積なので重力加速度が増減すれば重さも変わります。
この問題は、エレベーターに乗ったときに感じる浮く感じと床に押し付けられる感じの理由は、ニュートンの運動法則によるエレベーター内で体重計が増減する理由で簡単に説明しています。
私たちの日常感覚では北海道も東京も沖縄も同じ時間と空間ですが、超厳密に言えば違っています。 基準になる絶対空間が存在しないのですから、重力も空間によって変化すると考えるのでしょう。
重力を測る簡単な方法
重力とは質量がある物質が地球に引かれる力です。例えば、質量1g の物には1g dyne(ダイン)の重力が掛かっています。 ここで、gは比例常数(いつも同じ値をとる数値)で、重力加速度と呼ばれます。 (生活上は質量と重さを同義語に使うことがありますが、科学的には違うものです)
1dyne は質量1gの物体に働いて、1cm/s2の加速度を生じさせる力の大きさ。
1dyneは10万分の1N(ニユートン)
下垂振り子を使って重力加速度を測る
下垂振り子は、錘が下にぶら下がっている普通の振り子です。
この方法の測定で有名なのは、1790年のボルダ(J.C.Borda)の振り子です。
振り子の振れ幅が小さいときの振り子の周期 T(重りが振れて元の位置に戻るまでの時間)は
で表されます。ただし、π は円周率、Lは振り子の長さです。
この式の求め方にご興味があれば⇒ 微分方程式解法入門 単振り子の振動周期を求めるをご覧ください。
式(1)を重力加速度gで解くと
式2で解るように、重力加速度 g は、振り子の長さと周期(振り子が最初の運動状態になるまでの時間)が判れば求められます。
私は簡単な方法でどのくらいの値が出るのかやってみました。
先ず、錘の部分はネジのナット、それにぬい糸をつけて振り子とし、部屋の鴨居に釘を打って、その釘に振り子をつけて手で揺らせました。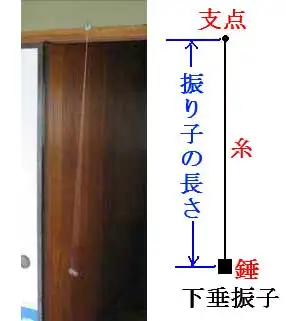
振り子の周期Tを測るのには、100円ショップで買ったストップウオッチを使い、 目で見てストップウオッチを押すといういい加減な方法ですがご参考になれば幸いです。
振り子の長さL= 1.08m
周期Tは、2.09 s(振り子を40回往復させて合計1分23.47秒だった)
式2の右辺にそれぞれの値を代入して重力加速度gを求めてみると
g = 9.76m/s2
と、かなり良い値が出ましたが、数回やってもこれ以上の値は出なかったのでまぐれですね。
物が落ちる時間を測定して重力加速度を求める
落下地点では発光ダイオードから出ている光が落ちて来た鉄球で遮られるのをフォトダイオードで検知します。
電磁石の電源を切った時に時計が動き出してフォトダイオードが光が遮られた瞬間に時計が停まるように電子回路を組みます。
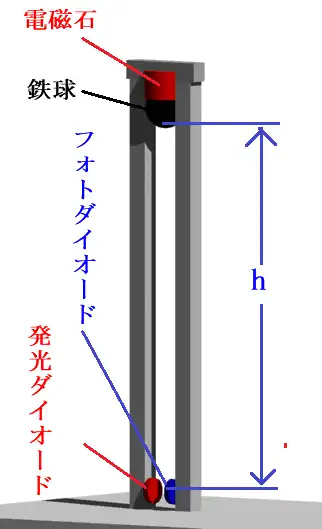
高さhの位置からhの基点0までに物が落ちる時間をtとします。
慣性系に於いては、動いている物の速度vは
で表されます。
ただし、v0は初速、αは加速度です。
物が落ちる時も同様で下向きを正とすると
t 秒間に落ちる距離 h は式3を時間 tで積分して
ここでは初速 v0は 0 なので式4は
式6から h メートル落ちる時間 t が判れば重力加速度 g が求められます。
しかし、実際に計測したつもりでダミーの値を入れて計算してみれば判りますが、非常に精密な時計が必要です。
重力の値が地球上の場所によって異なる理由
- 地球が完全な球でない
- 地球の内部構造が均一でない(鉱物やマグマなどが不均一にある)
- 地球が自転して遠心力が働く
- 太陽・月の影響を受けて海水や地下水が動いたり、地球の固体部分が変形する
- 雨により地下水の位置が変わる